Understanding fractions, particularly the concept of equivalent fractions, is crucial in mathematics. This article will meticulously explore which fraction is equivalent to 2/10, unravel different methods of determining equivalent fractions, and demonstrate the process through illustrative examples, ensuring a well-rounded comprehension for readers.
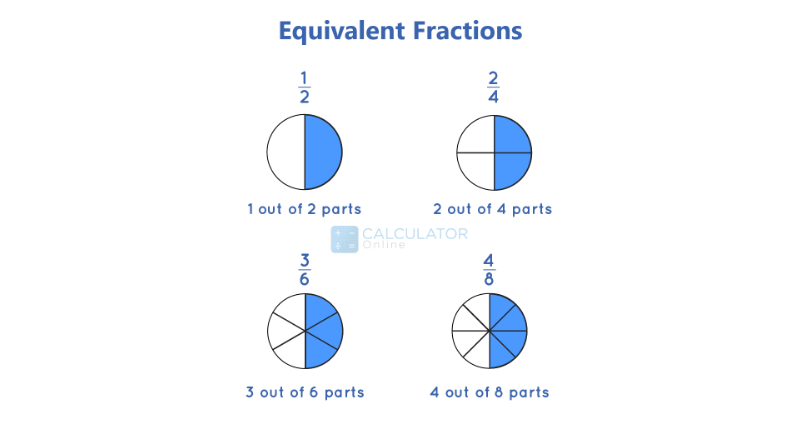
To ascertain which fraction is equivalent to 2/10, one must first recognize the definition of equivalent fractions. Equivalent fractions are those that may have different numerators and denominators but represent the same value when simplified. For instance, the fractions 1/2 and 2/4 are equivalent because they both express the same portion of a whole. This foundational understanding will guide our exploration.
The first crucial step in finding an equivalent fraction for 2/10 is to simplify this fraction. Simplification involves dividing both the numerator and the denominator by their greatest common divisor (GCD). Identifying the GCD of 2 and 10 will allow us to reduce the fraction to its simplest form.
The GCD can be determined through various methods, such as listing factors or utilizing the Euclidean algorithm. For 2 and 10, the factors are as follows:
- Factors of 2: 1, 2
- Factors of 10: 1, 2, 5, 10
From this list, it is evident that the greatest common divisor is 2. To simplify 2/10, each term must be divided by this GCD as shown below:
( frac{2}{10} = frac{2 div 2}{10 div 2} = frac{1}{5} )
Thus, the fraction equivalent to 2/10 is 1/5. However, this is merely one instance of equivalency. The beauty of fractions lies in the plethora of possible equivalent forms that can be generated through multiplication.
To generate additional equivalent fractions, one can multiply both the numerator and the denominator of 2/10 by the same non-zero integer. This strategy produces multiple fractions that, while different in appearance, represent the same value as 2/10.
For example, if we multiply both the numerator and the denominator by 2, we derive:
( frac{2 times 2}{10 times 2} = frac{4}{20} )
Similarly, multiplying by 3 yields:
( frac{2 times 3}{10 times 3} = frac{6}{30} )
Continuing this process, we could multiply by 4, resulting in:
( frac{2 times 4}{10 times 4} = frac{8}{40} )
By using larger multiples, one could arrive at more complex but equally valid equivalent fractions, such as 20/100 or 200/1000. The generaibility of equivalent fractions illuminates the vast possibilities within fractional arithmetic.
It is essential to recognize the contextual application of equivalent fractions in real-life scenarios. Fractions are prevalent in diverse fields such as cooking, financial mathematics, and scientific measurements. When recipes call for 2/10 of a cup of an ingredient, understanding the equivalency to 1/5 can simplify the cooking process, enabling easier measurements and adjustments.
Moreover, the comprehension of equivalent fractions greatly enhances one’s ability in algebra. For example, when resolving equations that involve fractions, recognizing equivalency allows for elegant simplifications and facilitates more straightforward solutions.
In addition to practical applications, equivalent fractions also encourage the development of critical thinking skills. By engaging with equivalent fractions, learners can cultivate analytical abilities—breaking down complex fractions into manageable parts and recognizing patterns within numerical relationships. This cognitive exercise nurtures mathematical reasoning, which is a fundamental skill extending beyond mathematics into various academic disciplines.
In summary, finding an equivalent fraction to 2/10 involves recognizing 1/5 as the simplest form through simplification. Additionally, numerous equivalent fractions can be created through multiplication, broadening the landscape of fractional representation. The utility of understanding equivalent fractions extends far beyond theoretical knowledge, encompassing practical applications across various disciplines and fostering critical cognitive skills in learners.
As one continues to explore the realm of fractions, maintaining a robust grasp of equivalency will undoubtedly serve as a valuable asset, enriching both academic pursuits and everyday life experiences. Whether it is in the kitchen or complex mathematical problems, the ability to identify and work with equivalent fractions enhances functionality and comprehension in any numerical context.
