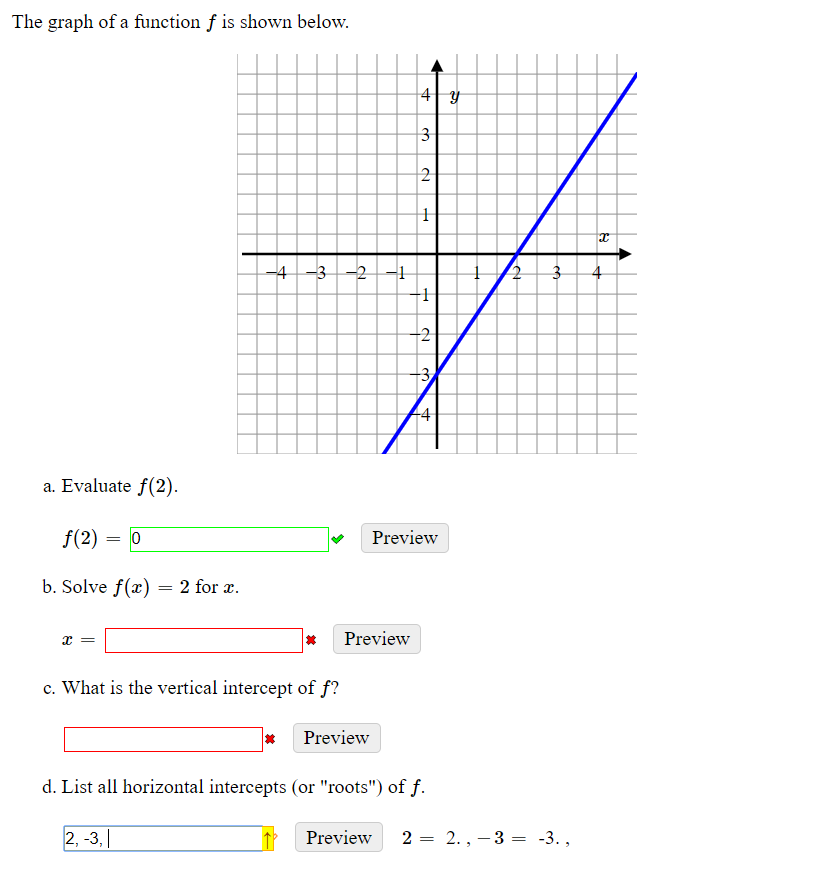
Graphical representations of functions often present an intriguing puzzle, captivating both novices and seasoned mathematicians alike. Picture yourself gazing at a myriad of lines, curves, and shapes, each vying for attention, beckoning you to unravel their mysteries. The quintessential question arises: “Which function is shown in the graph below?” This query invites contemplation and exploration, unleashing a journey into the realm of mathematical functions.
The pursuit of identifying a function begins with understanding the fundamental characteristics that define various types of functions. Functions can manifest in diverse forms, including linear, quadratic, polynomial, trigonometric, and exponential, each possessing distinctive features that differentiate them from one another. These characteristics can be analyzed in terms of their algebraic expressions, graphical representations, and behavioral tendencies.
To embark on this analysis, one must first assess the graph’s overall shape. Does it present a straight line, indicating a linear function? Alternatively, does it reveal a parabolic curve, suggesting a quadratic function? The process of elimination is an essential tool in the toolkit of any mathematician, allowing for the juxtaposition of possible candidates against the observed graph.
Linear functions, represented by the equation (y = mx + b), where (m) signifies the slope and (b) the y-intercept, yield straightforward graphs. A linear function’s most recognizable feature is its constant rate of change, producing a straight line extending infinitely in both directions. One might ask: Is the graphed function linear? If so, what do the slope and intercepts reveal about the relationships at play?
Transitioning to quadratic functions, we delve into (y = ax^2 + bx + c). The elegance of a parabolic curve opens a host of inquiries. Is the graph concave up or down? What are the vertex’s coordinates, the points of intersection with the x-axis, and the y-intercept? Each detail contributes to a comprehensive understanding of the function’s behavior. Quadratic functions epitomize symmetrical qualities, often producing two distinctive solutions when plotted.
Polynomial functions, extending beyond quadratics, introduce a more intricate structure with varying degrees. The leading coefficient’s sign and degree determine the graph’s end behavior, shaping whether it approaches infinity or negative infinity. The interplay of roots, turning points, and continuity defines polynomial characteristics, presenting a tantalizing challenge to identify their core expression. How many zeros does the graph exhibit? Could it be a polynomial function of higher degree or a combination of multiple functions?
In stark contrast, trigonometric functions introduce periodicity into the equation. These functions, characterized by sine, cosine, and tangent, progressively repeat their values, creating waves of delightful oscillations. Is the graph reflecting this enchanting cyclical behavior? Observing the amplitude and frequency can yield insights into the function’s identity. Does the wave crest at certain intervals, suggesting sine or cosine functionality? This fluidity in patterns invites deeper exploration of domains and ranges.
Exponential functions, typified by the form (y = a(b^x)), present another layer of complexity. Characterized by rapid growth or decay, an exponential function often defies linearity, instead exhibiting a distinctive accelerating curve. Is the graphed function manifesting exponential growth, or does it reveal exponential decay? Determining the base and initial value leads to recognizing its underlying characteristics. How does its asymptotic behavior shape our understanding of the function?
To add another dimension to our exploration, one must consider transformations of the basic functions. Graphs may display shifts, reflections, or dilations, complicating the identification process. A vertical or horizontal shift can fundamentally alter the function’s appearance while retaining its distinctive traits. Questions abound: How has this graph been transformed in relation to its parent function? What implications do translations have on the graph’s critical points?
Furthermore, piecewise functions emerge as fascinating entities, shattering the convention of singular expressions. These functions are defined by multiple sub-functions, each applicable to a specific interval. The graph’s appearance can change dramatically at boundary points, often producing a combination of linear, quadratic, or other types of functions within segments. Identifying these segments and transitions can become an elaborate challenge, requiring careful scrutiny of values and domains.
As one contemplates the graph before them, it is paramount to engage in a reflective practice. Take a moment to assess not only individual components but also the overarching essence of the function. Grasping the interplay between algebraic and graphical aspects enhances comprehension and enriches mathematical discourse. With each additional layer of understanding, the process becomes more gratifying, revealing the beauty and art of mathematics.
Ultimately, identifying the function represented in a graph is a formidable yet rewarding endeavor. Each inquiry propels one deeper into the complexities inherent in mathematical relationships, enriching the pursuit of knowledge. Whether grappling with linearity, curvature, periodicity, or more, the journey remains invigorating. Every graph has a story to tell, and through careful analysis, one can unearth its profound narrative, allowing mathematics to shine in its resplendent glory.
