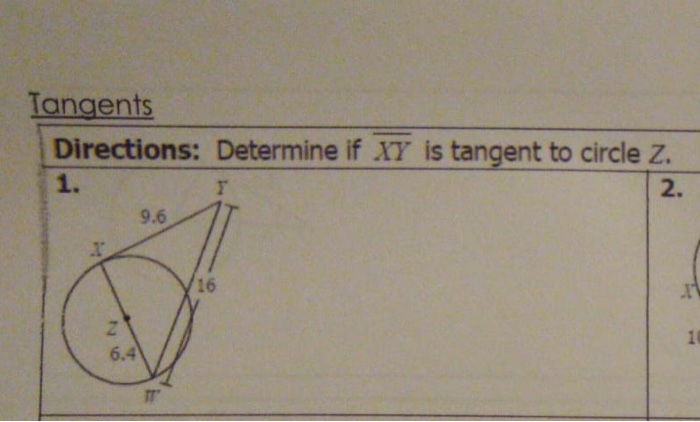
When grappling with the intricate relationships between lines and circles in Euclidean geometry, one may pose the question: “Which diagrams elucidate whether line XY is tangent to circle Z?” The challenge of determining tangency invites the analytical mind to delve deeper into geometric principles and visual representations. To thoroughly comprehend this dilemma, we must first examine the definitions involved, explore various scenarios, and finally analyze the diagrams representing these concepts. Each step will aid in unraveling the criteria for tangency and will sharpen our ability to discern complex geometric relationships.
In the realm of geometry, a tangent to a circle is defined as a line that intersects the circle at precisely one point. This unique point is known as the point of tangency. The significance of tangents extends beyond mere definitions; they have profound implications for understanding the properties of circles and the relationships among various geometric figures. With this concept in mind, we can set the stage for our exploration.
To determine if line XY is tangent to circle Z, several geometric principles should be considered. Additionally, the nature of the diagrams that accurately portray this relationship is paramount. Begin by envisioning the basic structure: a circle, traditionally represented as a perfect round figure, with its center denoted by a given point. Every point on the circumference is equidistant from this center, a property essential for our investigation into tangents.
Next, let us visualize line XY. When plotting this line in relation to circle Z, the positioning of XY dictates whether it shares a relationship of tangency with the circle. Various scenarios arise depending on how line XY interacts with the circle. Here are some crucial scenarios to consider:
- Scenario One: Line XY Intersects Circle Z at Two Distinct Points
In this scenario, line XY is not tangent to circle Z. When a line intersects a circle at two points, it is classified as a secant line. This distinction is critical, as it unequivocally asserts that the line cannot be a tangent. For visual representation, diagrams showcasing this case will exhibit line XY piercing the circumference of circle Z at two separate locations, distinctly marking the secant relationship. - Scenario Two: Line XY Intersects Circle Z at Exactly One Point
Herein lies the quintessential definition of tangency. Diagrams illustrating this scenario will depict line XY just grazing the circle at a singular point. This moment of contact is pivotal; the point at which the tangent touches the circle is marked clearly. Furthermore, a radius drawn from the center of circle Z to the point of tangency will be perpendicular to line XY, reaffirming its status as a tangent. This relationship uniquely defines the line’s distance from the circle, enhancing our understanding. - Scenario Three: Line XY Does Not Intersect Circle Z
The third scenario involves line XY completely bypassing circle Z, showcasing no intersection whatsoever. In this case, the line remains external to the circle’s perimeter. While line XY does not establish a tangential relationship here, it does suggest the line could potentially be tangent if it were to be repositioned to make contact at exactly one point. The diagrams portraying this case might illustrate line XY parallel to the circle’s tangent lines, hinting at a future interaction.
To accurately assess tangency through graphical representations, several critical geometric techniques must be employed. One common method involves calculating the distance from the center of circle Z to line XY. If this distance equals the radius of circle Z at the point of tangency, then line XY is confirmed as tangent. This calculation underscores the geometric interplay between radius, distance, and the positioning of external lines, enriching our understanding of tangents.
In addition to analytical methods, several diagrammatic elements must be incorporated to foster a comprehensive understanding of the situation. For clarity and precision, each diagram should include:
- A clear representation of circle Z, with its center marked.
- The exact coordinates of line XY in relation to the circle, including any significant intersection points.
- Notations indicating whether the line intersects zero, one, or two points on the circle.
- Perpendicularity notations where applicable, particularly in cases of tangents.
As we examine the diagrams depicting line XY in relation to circle Z, they serve as visual aids that can illuminate our understanding. Each case presents its own challenges and resolutions; however, true mastery comes from not only recognizing these diagrams but also from being able to create them based on given information. This skill empowers mathematical reasoning and enhances one’s capacity to analyze complex geometric relationships.
In conclusion, discerning whether line XY is tangent to circle Z requires a confluence of theoretical knowledge and practical analysis. By contemplating distinct scenarios, employing geometric calculations, and scrutinizing foundational principles, one can unravel the complexities surrounding tangency. Therefore, next time you encounter such a geometric challenge, resolve to visualize your problem clearly, reflect on the principles of tangency, and leverage your diagrammatic skills to clarify your understanding. The beautiful interplay of geometry awaits your exploration!
