Understanding the concept of congruent angles is pivotal in the study of geometry, particularly when examining their properties and relationships. To explore the question, “Which angle is congruent to 1?” we delve into the foundational elements of angles, the types of angles, and the principles governing their congruence. By the end of this discussion, readers will be equipped with profound insights into how angles mirror each other in various geometric contexts.
To commence our exploration, it is essential to define congruence in the geometric realm. Congruent angles are angles that have equal measures. If angle A measures 45 degrees, any angle that also measures 45 degrees is congruent to angle A, signifying a profound symmetry in their angular expanse. This reflection of measurement is crucial in constructing geometric proofs and solving intricate mathematical problems.
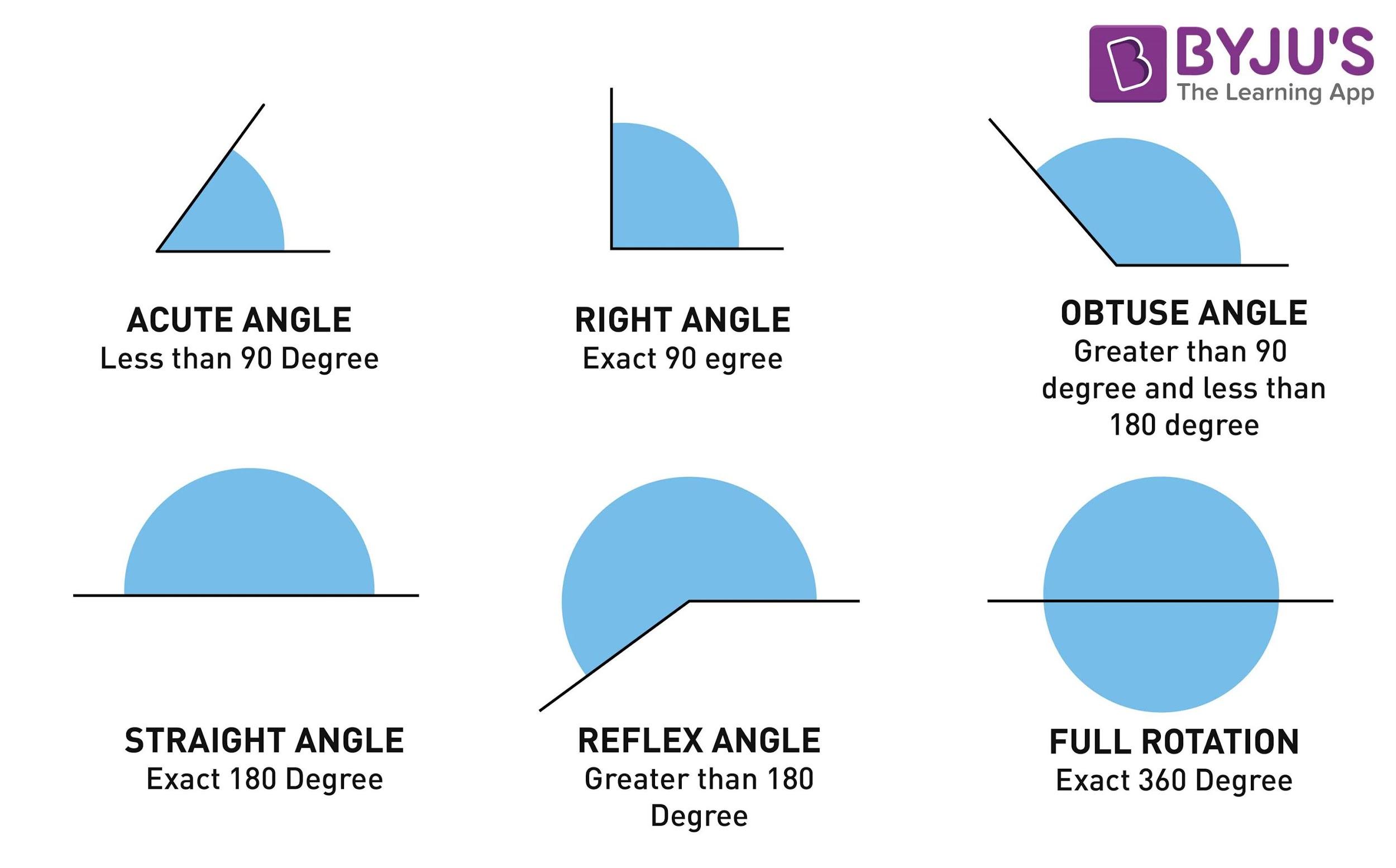
Next, we will categorize angles into distinct types, each encompassing unique characteristics yet sharing the fundamental property of congruence among peers:
- Acute Angles: Accomplishing the delicate balance of being less than 90 degrees, acute angles are conversely larger than 0 degrees. Two acute angles can be congruent if they share an identical degree measurement, such as 30 degrees. This subtle definition encourages a deeper appreciation for the minute differences that separate acute angles, yet emphasize their potential for congruence.
- Right Angles: A right angle is quintessentially set at 90 degrees. Being uniform across its definition, any angle recognized as a right angle inherently mirrors others characterized by the same measure. Therefore, if we were to ponder which angle is congruent to a specified right angle, the answer is straightforward: it is any angle securing the measure of 90 degrees.
- Obtuse Angles: These angles bask in the glory of exceeding 90 degrees but remaining shy of 180 degrees. Similar to their acute counterparts, obtuse angles can achieve congruence by collaborating on identical measurements, such as 120 degrees. The nuances of obtuse angles also showcase the breadth of geometric possibility.
- Straight Angles: Defined as angles featuring a measure of 180 degrees, straight angles are instrumental in numerous geometrical applications. The congruence among straight angles is easily identified as any angle measuring 180 degrees is congruent to every other angle bearing the same measurement, reinforcing the simplicity central to their evaluation.
- Reflex Angles: These intriguingly broad angles exceed the 180-degree threshold yet do not quite reach 360 degrees. Congruent reflex angles are those that are equal in magnitude, such as two angles each measuring 250 degrees. Understanding these angles requires a careful synthesis of their measures and properties.
As we navigate through the various types of angles, it becomes crucial to introduce the concept of complementary and supplementary angles. Complementary angles, where the sum of the two equals 90 degrees, provide a fertile ground for congruence. For example, if angle B is 40 degrees, its complementary angle C must be 50 degrees for congruence to be introduced at later angles.
In light of supplementary angles, where two angles sum to 180 degrees, congruence manifests in alternative pairs as well. If angle D measures 70 degrees, its supplementary angle E must measure 110 degrees to maintain the equilibrium of totality and simultaneously adhere to congruence when encountering various transformations.
Often, angles are co-interior angles, alternate interior angles, or corresponding angles formed when a transversal intersects two parallel lines. These relationships yield congruence through the lens of geometric theory. For example, when two parallel lines are intersected by a transversal, the corresponding angles remain congruent, establishing a foundational principle utilized across numerous geometric proofs.
In practical applications, recognizing congruent angles proves invaluable in architectural design, engineering, and various technology sectors. Accurate alignment and congruence are paramount in creating structurally sound and aesthetically pleasing designs. Designers, engineers, and architects often employ congruence in evaluating risk, enhancing stability, and ensuring the integrity of their constructs.
In conclusion, the quest to comprehend which angle is congruent to angle 1 invites us into the ornate world of angle relationships. By categorizing angles into acute, right, obtuse, straight, and reflex, we glean a comprehensive understanding of their potential for congruence. Moreover, through complementary, supplementary, and transversal angles, we discover additional layers of symmetry and balance. These principles, when aptly applied to real-world scenarios, reaffirm the importance of congruence in maintaining accuracy and equilibrium across varied fields. Engaging with these concepts equips individuals not only with knowledge but also with the tools necessary to excel in geometrical reasoning.
