Understanding geometric principles is crucial for mastering the intricacies of shapes, angles, and their relationships. One fundamental aspect of geometry involves defining congruence, particularly concerning angles. This article delves into the notion of congruent angles, elucidating their properties and relationships, especially in the context of “3-Mastering Geometry Symmetry.” Through discussions on various types of angles and applications in geometric symmetry, readers will cultivate a comprehensive comprehension of this essential topic.
Defining Congruent Angles
Congruent angles are angles that have identical measures. When two angles are congruent, they can be superimposed directly onto one another without any discrepancies in their dimensions. This concept forms the cornerstone of numerous geometric proofs and applications. In the realm of geometry, understanding congruence not only aids in solving problems but also illuminates the relationships between various geometric figures.
Types of Angles
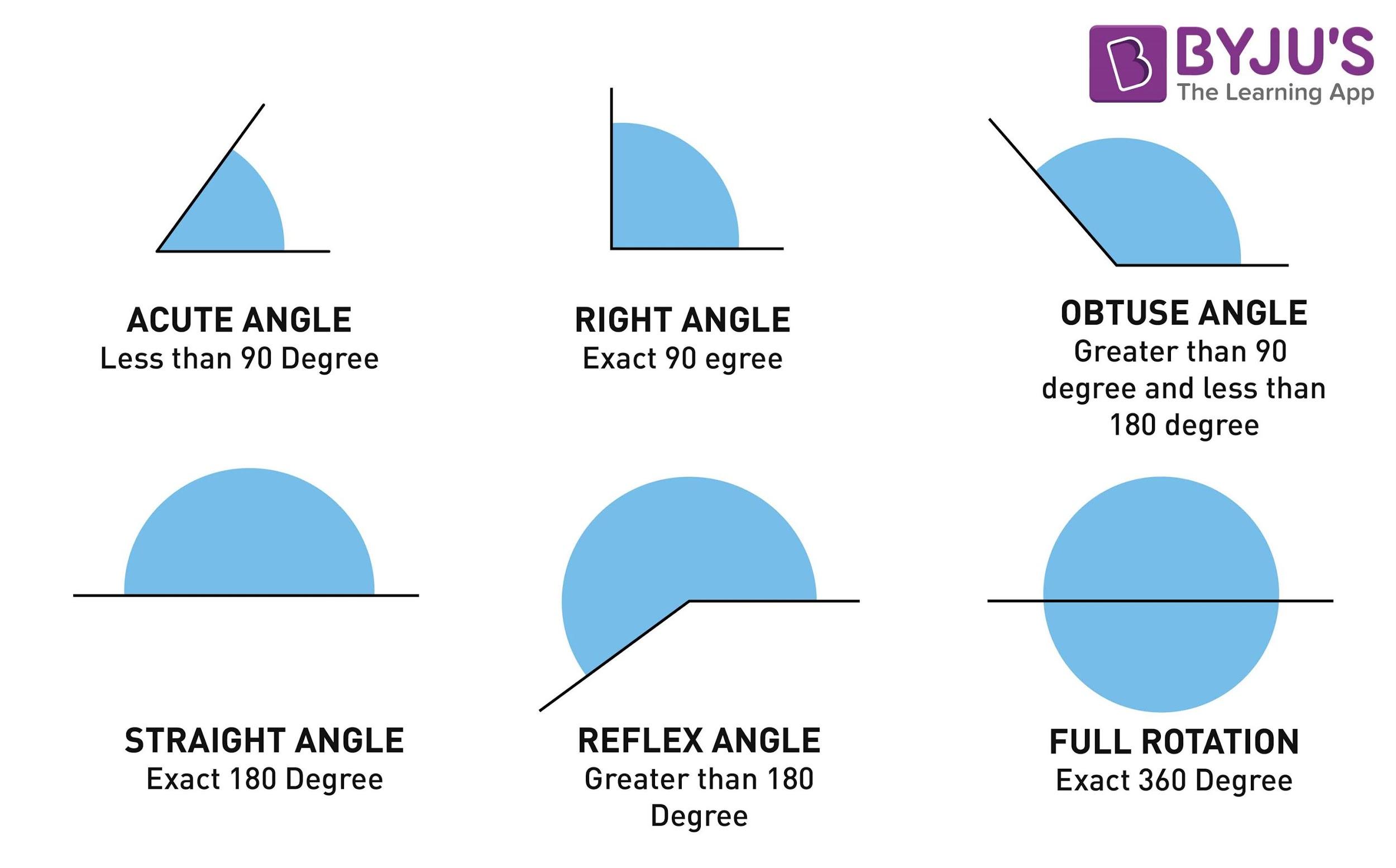
To appreciate which angle is congruent to a specific angle, one must first delve into the classifications of angles. The primary types of angles include:
- Acute Angle: An angle measuring less than 90 degrees.
- Right Angle: An angle exactly equal to 90 degrees.
- Obtuse Angle: An angle more than 90 degrees but less than 180 degrees.
- Straight Angle: An angle that measures exactly 180 degrees.
- Reflex Angle: An angle measuring more than 180 degrees and less than 360 degrees.
These classifications serve as a foundational understanding of angles, allowing us to analyze their properties and establish congruence with precision.
Angle Relationships and Congruence
In various geometric configurations, angles can display congruence through specific relationships. Such relationships include:
- Vertical Angles: Formed when two lines intersect, vertical angles are always congruent. For example, if two intersecting lines create angles of 30 degrees and 30 degrees opposite each other, these angles are congruent.
- Adjacent Angles: Share a common side and vertex. While adjacent angles are not always congruent, two adjacent angles can be congruent if they measure the same.
- Complementary Angles: Two angles are complementary if their sum equals 90 degrees. If one angle measures 40 degrees, its complementary angle must measure 50 degrees; they are not congruent but related.
- Supplementary Angles: Two angles are supplementary if their sum equals 180 degrees. If two supplementary angles measure 60 degrees and 120 degrees, they are not congruent either.
Understanding these relationships allows us to deduce conformance and recognize congruent angles through various configurations in geometric setups.
Symmetry in Geometry
The concept of symmetry plays a pivotal role in determining congruence relationships among angles. Symmetry can be observed in various forms, including reflectional and rotational symmetry. Understanding these principles can assist in mastering geometry symmetry within the context of congruent angles:
- Reflectional Symmetry: A shape exhibits reflectional symmetry if one half is a mirror image of the other. In such shapes, corresponding angles are congruent. For example, in an isosceles triangle, the angles opposite the equal sides are congruent.
- Rotational Symmetry: A shape is said to have rotational symmetry if it can be rotated to match its original configuration. With rotational symmetry, the angles subtended at each corner can often be congruent. Regular polygons exhibit this kind of symmetry strongly.
Symmetry not only enhances aesthetic appeal but also provides insights into various geometric properties, facilitating a deeper understanding of congruence among angles.
Application of Congruent Angles in Problem Solving
In practical geometric problems, recognizing congruent angles is essential. Problems often require identifying congruencies to deduce unknown angle measures, thus relying on established relationships discussed previously. For instance, in the case of intersecting lines, knowing that vertical angles are congruent allows one to equate measures and solve for unknowns efficiently.
Furthermore, congruent angles are critical in constructions and proofs. The Angle Addition Postulate, for example, asserts that if a point lies on the interior of an angle, the sum of the two adjacent angles formed is equal to the measure of the larger angle. This principle plays a significant role in various mathematical proofs encountered in higher levels of geometry.
Culminating Insights
Mastering the concept of which angle is congruent to another requires a rich understanding of the properties and relationships that govern angles in geometry. By comprehensively exploring the types of angles, their congruence relationships, and the insights provided by symmetry, one can navigate through complex geometric challenges with enhanced acuity. Geometry serves as an intricate tapestry woven with the thread of congruence, allowing learners to appreciate the beauty and logic inherent in mathematical reasoning.
Ultimately, a profound grasp of congruence among angles fosters not only academic proficiency but also a deeper appreciation for the patterns that exist within the realm of geometry, further enriching one’s mathematical journey.
