The study of angles and their relationships is a fundamental aspect of geometry, a branch of mathematics that extends far beyond mere calculations. Among the myriad types of angle relationships, one particularly fascinating category is that of vertical angles. Typically, identifying vertical angles can seem daunting, but with a proper understanding and visualization techniques, it becomes a thoroughly engaging experience.
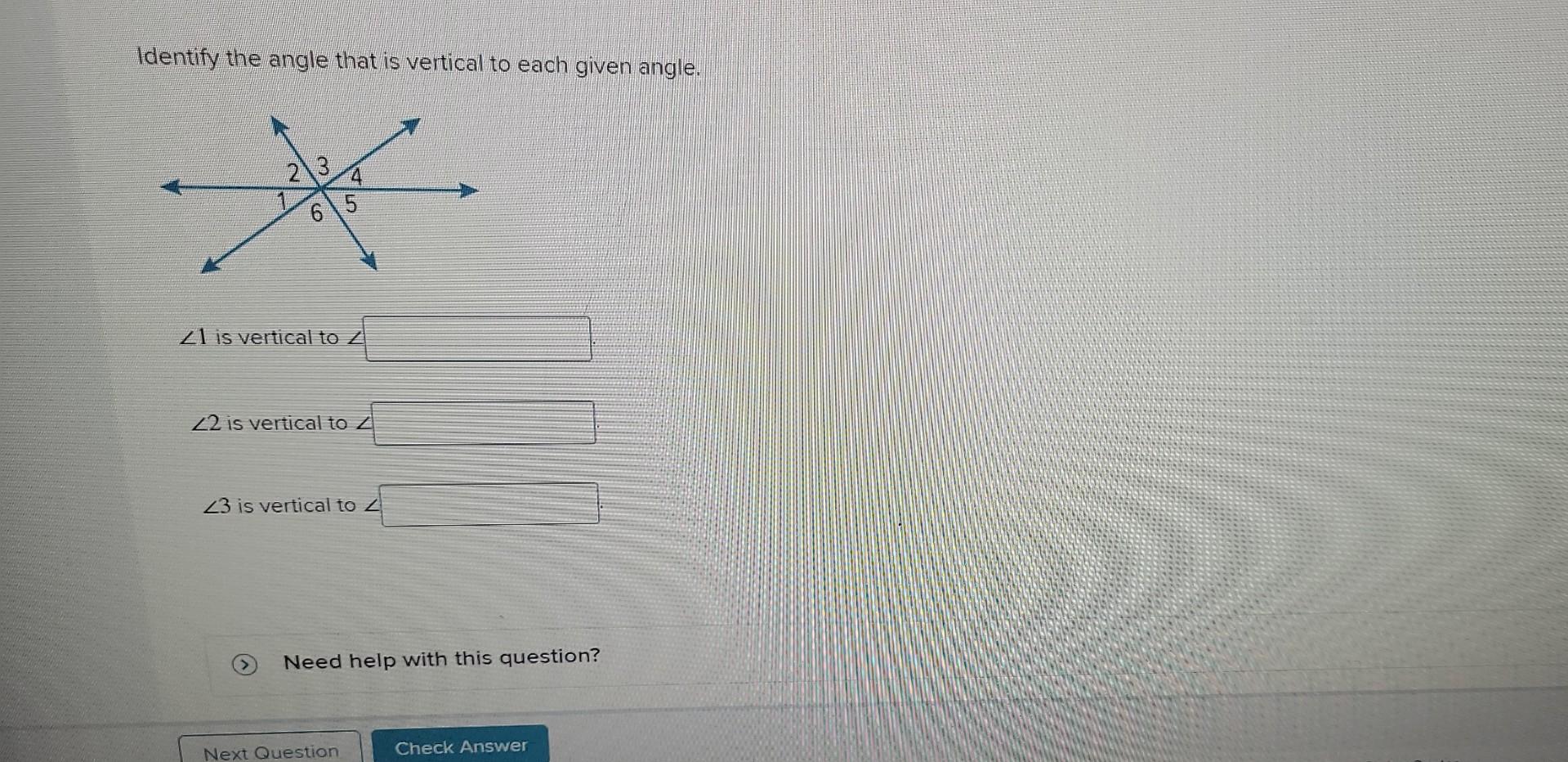
To initiate the exploration, we must first elucidate what vertical angles are. Vertical angles emerge when two lines intersect, creating pairs of angles across from each other. This relationship is not just a trivial aspect of geometry; vertical angles are equal in measurement, a fact that instigates deeper inquiries into their implications in mathematical reasoning and real-world applications.
The crux of understanding vertical angles lies in visualizing angle relationships. When two lines intersect, they divide the plane into four distinct angles. Among these angles, pairs that are formed at opposing corners are considered vertical. For instance, if we denote the intersection points as A, B, C, and D, with angle ACB being vertical to angle DCA, they share a specific equality property: ACB = DCA. This realization leads to a myriad of inquisitive thoughts about why such relationships exist and what underpins their nature.
One common observation among students and enthusiasts alike is the innate symmetry present in vertical angles. This immaculate aspect presents an aesthetic allure that can captivate the mind. The very act of visualizing or drawing intersecting lines can evoke a sense of order and balance, reminiscent of the principles found in nature and art. For instance, consider the symmetry in the branches of a tree or the architectural elegance of bridges—these forms often adhere to principles that echo those of vertical angles.
To accurately visualize these relationships, employing a diagram can be beneficial. Begin with two intersecting lines—label them as Line 1 and Line 2. Mark the angles formed at the intersection, ensuring that you systematically denote each angle by its respective vertex. Upon closer inspection, you will notice the two pairs of vertical angles emerging. It becomes clear that if one angle measures, say, 50 degrees, the opposite angle across will also measure 50 degrees. This lucid example serves as an anchor for deeper investigations into angle relationships.
Digging deeper, one may ponder the application of vertical angles in various real-world contexts. Architecture and engineering fields utilize these principles extensively. Whether one is designing a skyscraper or constructing a complex bridge, understanding how angles interact is crucial. Vertical angles further reinforce structural integrity. For example, the angles at an intersection point can influence the load distribution and stability of a structure. Thus, the practical applications of understanding vertical angles extend into meaningful geometrical constructs that affect daily life.
Moreover, vertical angles play a role in trigonometry and coordinate geometry. A solid grasp of vertical angles lays a foundational understanding necessary for more complex problems, including those involving alternate interior angles and transversal intersections in parallel lines. This interconnection among various mathematical concepts illustrates the rich tapestry that geometry weaves, wherein vertical angles serve as a crucial thread binding numerous principles together.
The educational implications of vertical angles cannot be overstated. Developing strategies to teach these concepts effectively is pertinent. For instance, using interactive software or geometric modeling tools can enhance student comprehension significantly. Engaging students through games involving angle estimation or utilizing dynamic geometry software to manipulate angles can foster an appreciation for the beauty evident in the relationships between angles. Such methodologies can shift a student’s perspective from viewing these concepts as mere rote memorization to experiencing them as dynamic interconnections that inspire curiosity.
Furthermore, utilizing storytelling techniques to explain vertical angles can add an engaging element to learning. By anthropomorphizing angles as characters that interact with one another, educators can create a narrative around the principles of verticality. For instance, illustrating a dialogue between angles as they compete for equality can spark intrigue among learners. This creative approach invites students to exercise their imagination while simultaneously embedding vital concepts in their understanding.
In summary, the inquiry into vertical angles is not merely an academic exercise; it reveals a fundamental harmony present in the universe of geometry. By engaging with the observation of vertical angles, one can appreciate the aesthetic symmetry they offer, uncover their practical applications, and appreciate their integral role in various branches of mathematics. Moreover, teaching methods that incorporate visualization and storytelling can enhance the learning experience, transforming the abstract into the tangible. Through this multi-faceted exploration, we gain insight not only into the properties of vertical angles but also into a broader understanding of the intricate relationships that govern our mathematical environment.
In conclusion, the question, “Which angle is vertical to 1?” transcends basic identification; it invites a deeper investigation into the nature of angles themselves. Thus, as you visualize and analyze various angle relationships, take a moment to appreciate the underlying beauty and symmetry that they create, inviting endless possibilities for exploration.
