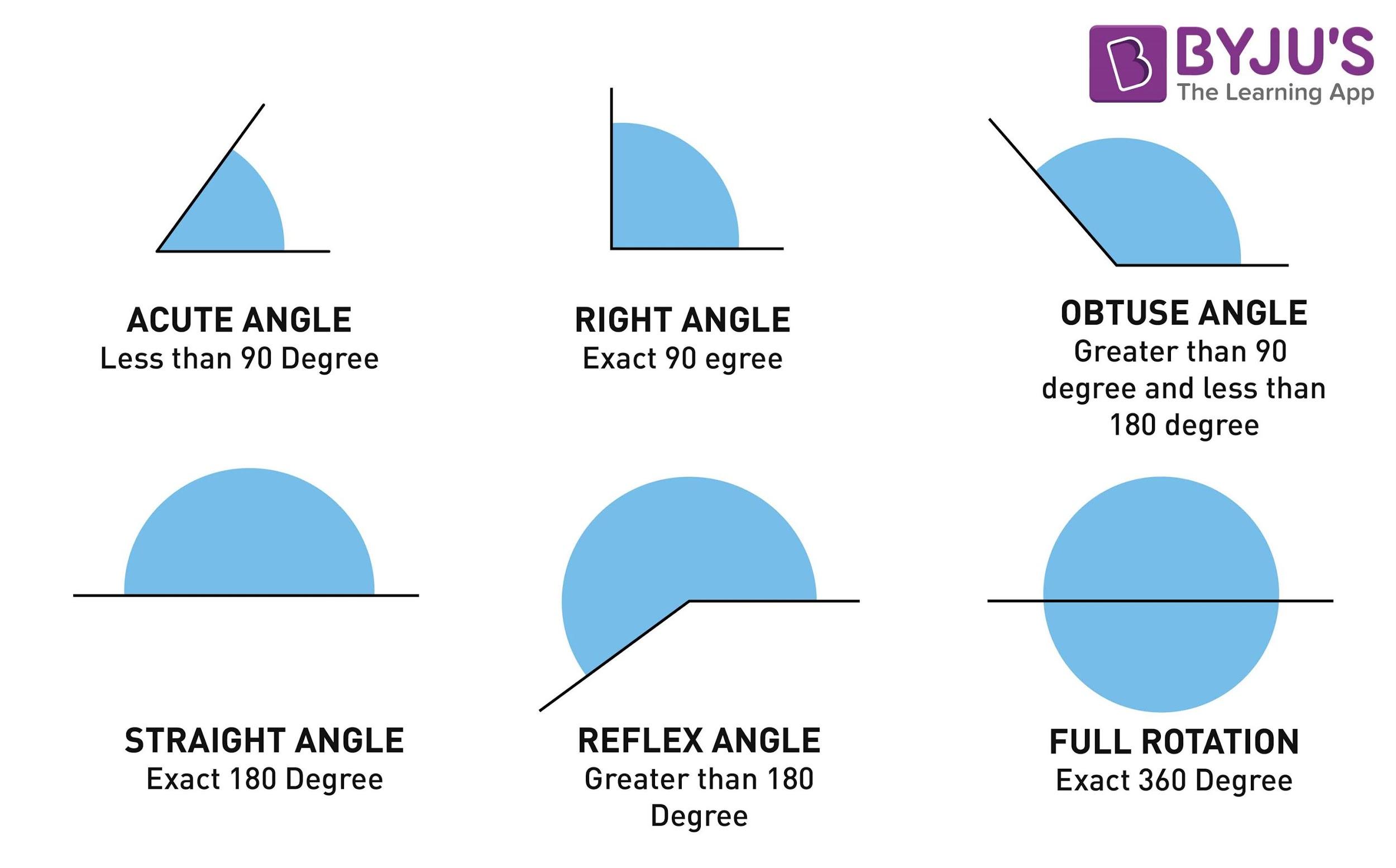
Angles are fundamental constructs in geometry that enable the exploration of diverse spatial relationships. They connect lines and planes in a myriad of configurations. Among the myriad types of angles, vertical angles hold a special significance that transcends simple geometric calculations. They embody a fascinating interplay between spatial orientation and angular measures. But how do we truly grasp which angle is vertical to another? Let’s delve into this intriguing topic and uncover the connections between vertical pairs through five enlightening discoveries.
To embark on our journey, we will first clarify what vertical angles are. Vertical angles arise when two lines intersect, creating pairs of opposite angles. By definition, these angles are congruent, which means they share the same measure. This foundational tenet of vertical angles introduces a playful challenge: can you visualize the situation where multiple intersecting lines create a myriad of angles, yet only specific pairs are deemed vertical? As we proceed, we will explore this interplay through five pivotal discoveries.
1. Understanding the Intersection of Lines
Before defining vertical angles, it is imperative to understand the mechanics of line intersections. When two lines cross each other, they form two pairs of angles. For example, consider lines A and B intersecting at a point. Here, we generate four angles: Angle 1, Angle 2, Angle 3, and Angle 4. To determine the vertical angles, simply identify the angles across from each other, which are Angle 1 with Angle 3 and Angle 2 with Angle 4. This leads to an essential discovery: recognizing the relationship among intersecting lines offers a foundation for understanding various angle pairs.
2. The Congruence of Vertical Angles
The remarkable quality of vertical angles lies in their congruence. Regardless of the inclination or orientation of the intersecting lines, the angles formed in opposite positions will always possess equal measures. This principle raises another question: how can this knowledge be applied in practical scenarios? For example, architects and engineers utilize the property of vertical angles in their designs, ensuring structural integrity and aesthetic harmony. By comprehensively understanding the congruence of vertical angles, practitioners across various fields can make informed decisions regarding spatial arrangements.
3. Visual Representations of Vertical Angles
Visual learning is an effective approach for grasping complex concepts. Utilizing diagrams and illustrations enhances the comprehension of vertical angles, allowing individuals to see the symmetries and congruences at play. Consider a simple intersection of two lines, where the measures of the angles can be annotated. Such representations clarify how angles 1 and 3 correspondingly relate, providing an invaluable visual cue for learners. Moreover, exploring digital tools that simulate angle formation can foster deeper insights, engaging learners through interactivity and reinforcing their understanding of angle relationships.
4. Applications in Real-World Problem Solving
The utility of vertical angles extends far beyond academic confines. In navigation and construction, understanding vertical angles can prove instrumental. For instance, when laying out foundations or creating blueprints, insights into the relationships of vertical angles can inform decisions regarding materials and angles of elevation. This discovery compels the observer to contemplate a challenge: can one utilize the principles of vertical angles to solve real-world dilemmas? As professionals and students alike grapple with practical situations, the lessons learned from vertical angles emerge as indispensable tools in their arsenal.
5. Exploring Complex Angle Relationships
Finally, mastering the vertical angle concept prepares individuals for advanced geometric studies. Once the basics have been mastered, exploring complex relationships among multiple angles—such as adjacent, complementary, and supplementary angles—becomes feasible. Identifying vertical angles can serve as a stepping stone into more intricate explorations of angular relationships. Can you imagine how these connections weave through mathematical theories and applications? By posing such questions, we invite a broader consideration of the implications of vertical angles, integrating them into the larger tapestry of geometry.
As we conclude our exploration of vertical angles, a cogent understanding emerges regarding which angle is vertical to another. Through the prism of our five discoveries, we have illuminated the neighborly connections of vertical pairs, explored their inherent congruence, and acknowledged their practical applications. One cannot help but appreciate the elegance found within these angular relationships. The challenge lies in fully grasping their implications and harnessing this knowledge for practical and theoretical mastery. As students and professionals alike confront the intricate world of angles, vertical pairs will undoubtedly remain a pivotal facet of their journey through the geometric landscape.
