Angles are fundamental components of geometry that play a significant role in understanding the relationships between various geometric figures. One particularly interesting aspect of angles is the concept of corresponding angles. But what exactly are corresponding angles? How can one identify them? Are there particular types of angles that stand out as corresponding angles? Let’s explore this intriguing topic, dissecting definitions, properties, and applications of corresponding angles.
To begin our journey into the world of angles, let us pose a playful question. Imagine you are surveying a pair of parallel lines sliced through by a transversal. What might you discover about the angles created at the intersections? This scenario sets the stage for our understanding of corresponding angles. The challenge lies in identifying these angles amidst a plethora of angle types. Are you ready to uncover the secrets?
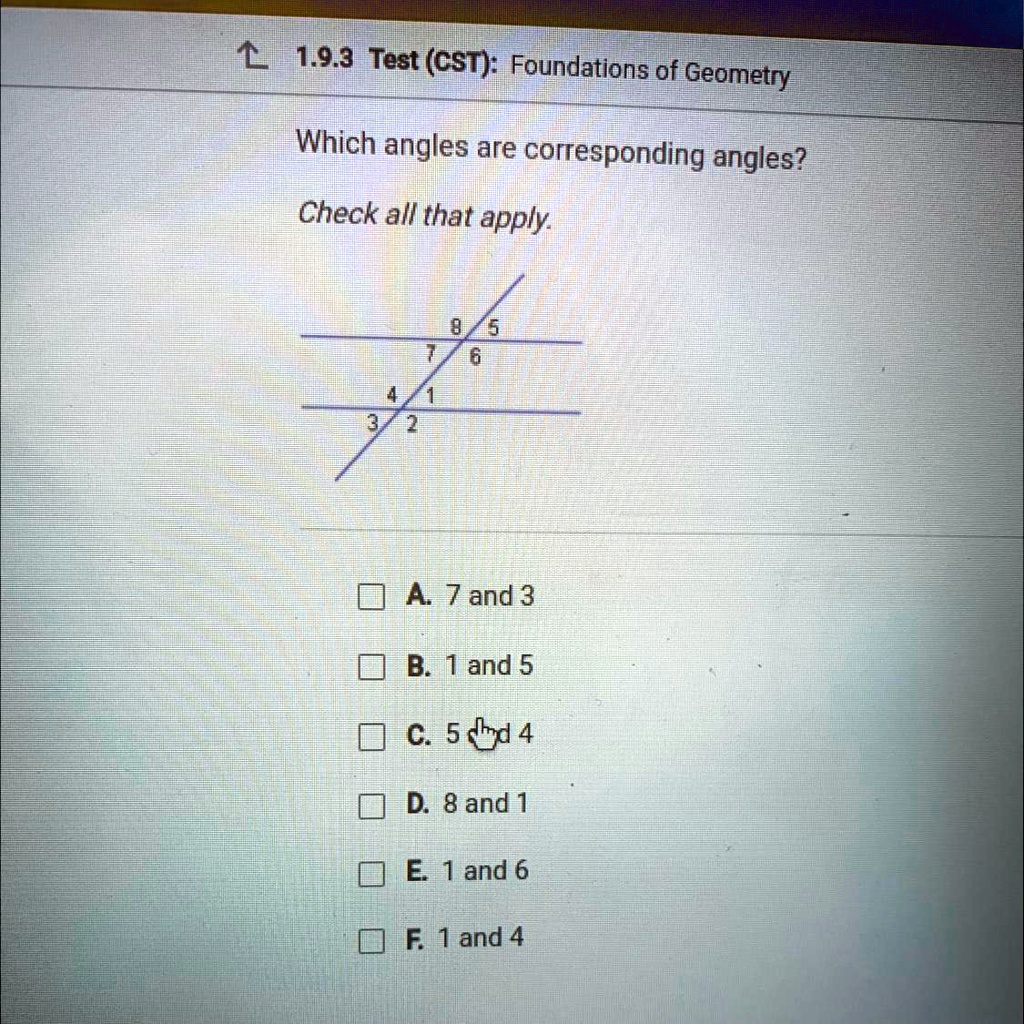
Corresponding angles are defined as the angles that occupy the same relative position at each intersection where a transversal crosses parallel lines. It is essential to bear in mind that for two angles to be corresponding, they must not only be formed by the intersection of a transversal and parallel lines, but they must also match in position. For instance, if a transversal intersects a pair of parallel lines, angle one on one line corresponds to angle two on the other line. The positioning is paramount—angles must fabricate the same position across parallel constructs.
Now, let us delve into the characteristics of corresponding angles. One of the most significant properties is that corresponding angles are congruent when formed by parallel lines and a transversal. This means they are equal in measure. Therefore, if angle A and angle B are corresponding angles, the measure of angle A will be identical to the measure of angle B. This property is not merely theoretical; it possesses practical implications in various fields such as architecture, engineering, and even art.
For clarity, let us categorize the circumstances under which angles will qualify as corresponding angles. When you have two parallel lines cut by a transversal, look for the following pairs of angles that you can designate as corresponding:
- Angle in the upper-left position of the first intersection: This angle will correspond to the angle in the upper-left position of the second intersection.
- Angle in the upper-right position of the first intersection: Look for the angle in the upper-right position of the second intersection; these two angles correspond as well.
- Angle in the lower-left position of the first intersection: This angle corresponds to the lower-left angle at the second intersection.
- Angle in the lower-right position of the first intersection: Don’t forget to look at the lower-right angle of the second intersection for correspondence.
To visualize these concepts more concretely, consider the following scenario. Take two parallel lines labeled A and B, and introduce a transversal named T. The points of intersection generate four distinct angles on each line. By meticulously analyzing these intersections, one can easily identify the corresponding angles as described above. This is not merely an academic exercise; it is instrumental in deciphering complex geometric problems.
In the realm of geometry, corresponding angles offer more than just theoretical insights; they extend into applications and real-world phenomena. For example, in architecture, understanding corresponding angles is integral when designing structures to ensure that various elements align correctly. Similarly, in navigation and surveying, corresponding angles allow for appropriate mapping and alignment of positions relative to one another. Such principles emerge in practical scenarios, illustrating the ubiquity of corresponding angles beyond the confines of the classroom.
As we navigate through this exploration of corresponding angles, it is essential to fixate on identifying potential challenges. What if the lines are not parallel? In such cases, corresponding angles would not be congruent, and one should tread carefully. This deviation from parallelism introduces a layer of complexity, creating angles that may interact differently. It is crucial to remember that the core principle of corresponding angles rests upon the unwavering premise of parallel lines intersected by a transversal.
In conclusion, the exploration of which angles qualify as corresponding angles presents an intellectual challenge that intertwines various facets of geometry. By identifying corresponding angles, one not only enhances their geometric understanding but also equips oneself with analytical tools that are applicable in various domains. Next time you encounter parallel lines and a transversal, recall the angles you can classify as corresponding, and embrace the beauty of geometry that surrounds us daily. Let this knowledge empower your mathematical journey as you unravel further mysteries of the geometric world!
