Geometry, the branch of mathematics concerned with the properties and relations of points, lines, surfaces, and solids, is fundamentally intertwined with our everyday experiences. Among its many fascinating components, angles stand out due to their ubiquitous presence in the natural and man-made world. To master geometry is, in many ways, to master angles; but which angles can be classified as right angles? This inquiry forms the crux of understanding basic geometry and serves as a gateway to further exploration of geometric principles.
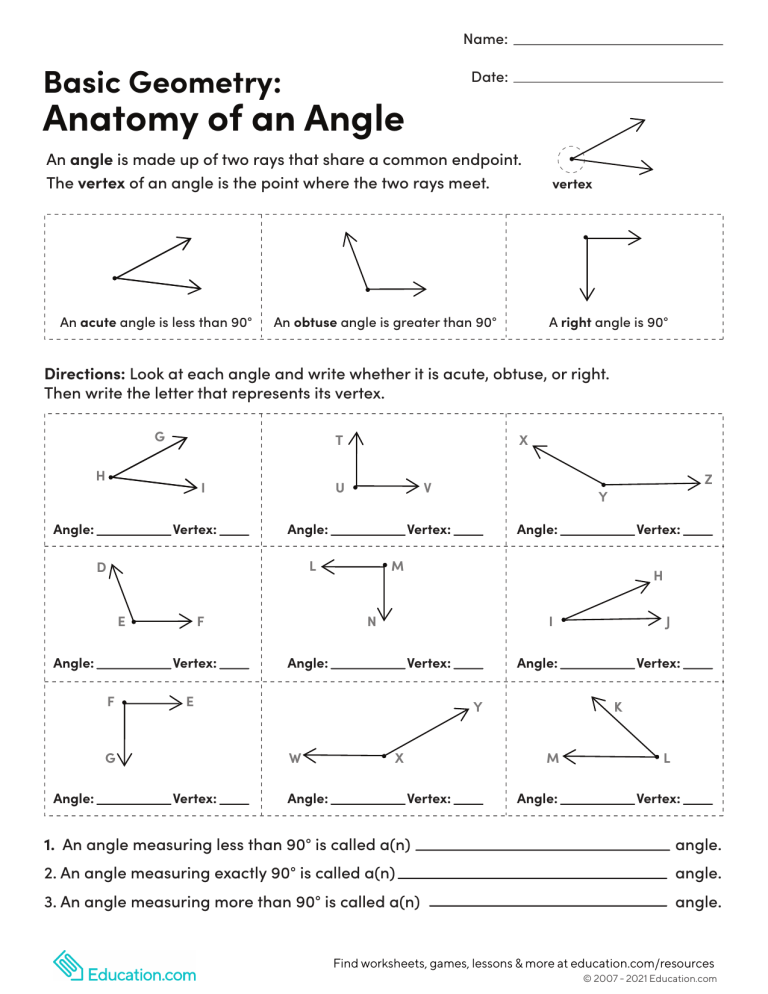
To navigate through the complexities of angles and their classifications, we begin by defining what constitutes a right angle. A right angle is defined as an angle that measures exactly 90 degrees, forming a perfect L-shape when visualized. This specific measurement evokes a sense of precision and balance. Right angles are indeed the building blocks of many geometric shapes and the standards against which other angles are measured.
There are several types of angles that may be encountered. Each has its unique characteristics and formulas, enabling us to discern right angles from the myriad of possibilities. Here, we provide a comprehensive exploration of the various angles you may encounter while checking for right angles.
Types of Angles: An Overview
1. **Acute Angles**: An acute angle measures less than 90 degrees. These angles are often found in acute triangles and convey a sense of sharpness or precision. They do not qualify as right angles, which invariably are defined by their specific 90-degree measurement.
2. **Obtuse Angles**: Conversely, obtuse angles surpass 90 degrees but fall short of 180 degrees. These angles often evoke feelings of expansiveness and can create visually striking designs in architecture but, like acute angles, they cannot be classified as right angles.
3. **Straight Angles**: Measuring exactly 180 degrees, straight angles represent a linear form rather than a right one. While they are a critical component of various geometric configurations, they do not fulfill the criteria established for right angles.
4. **Reflex Angles**: Reflex angles are those that exceed 180 degrees but are less than 360 degrees. These angles may appear fascinating due to their larger-than-life presence, yet they too fall outside the definition of right angles.
5. **Right Angles**: The stalwart of our discussion, right angles, possess that vital characteristic of measuring exactly 90 degrees. They can often be identified in numerous everyday settings—think of the corners of a book or the junctions of walls in a room. Recognizing right angles enables individuals to grasp the essence of many geometric configurations.
Overall, the classification of angles into these categories is not merely academic—it has profound implications for practical application, such as in construction and design. Establishing precise angles ensures structures are stable and functional, which further captivates students and enthusiasts alike with an appreciation for geometry’s role in the tangible world.
Identifying Right Angles: Techniques and Tools
Recognizing right angles involves a variety of techniques and tools. Knowledge of these methods can enhance your exploration in geometry and deepen your understanding of its fundamental principles.
1. **The Protractor**: A quintessential tool in any geometry kit, the protractor measures angles in degrees, allowing users to ascertain whether an angle is right. By aligning the baseline of the protractor with one ray and checking the measurement against the scale, one can quickly confirm the angle’s classification.
2. **The Carpenter’s Square**: Commonly used in woodworking, this tool is invaluable for confirming right angles in the construction process. The square’s distinctive L-shaped design assists craftsmen in ensuring that corners are perfect right angles.
3. **Visual Indicators**: Sometimes, visual cues can offer insight. A right angle will create a recognizable L-shape, which can be observed in various everyday contexts. Though not always precise, visual recognition serves as a helpful heuristic for initial assessments.
4. **Coordinate Geometry**: In a more advanced explorative realm, the use of coordinate systems allows for geometric calculations to determine angles. By employing the slope of lines in a Cartesian plane, one can calculate angles formed between intersecting lines and verify if any are indeed right angles.
The Importance of Right Angles in Geometry
Understanding right angles is not merely an academic exercise; it also provides foundational knowledge essential for advanced geometrical concepts and real-world applications. For example, the Pythagorean theorem, often expressed as a² + b² = c², is predicated on the existence of right angles. This theorem has far-reaching implications in mathematics, physics, engineering, and even computer science, highlighting the practical relevance of right angle comprehension.
Furthermore, right angles serve as a frame of reference in creating various geometric shapes, including rectangles, squares, and right triangles. These shapes regularly surface in architectural designs and artwork, revealing an aesthetic that resonates deeply with our innate preferences for symmetry and order.
Conclusion
In summary, angles form a core component of geometry, and right angles are pivotal to mastering this discipline. Differentiating between types of angles can pose occasional challenges, yet identifying right angles offers a straightforward way to solidify understanding and build a pathway towards more complex geometric theories. Through both mathematical rigor and practical application, the appreciation of right angles unfurls a deeper appreciation for the elegance of geometry that governs our world.
