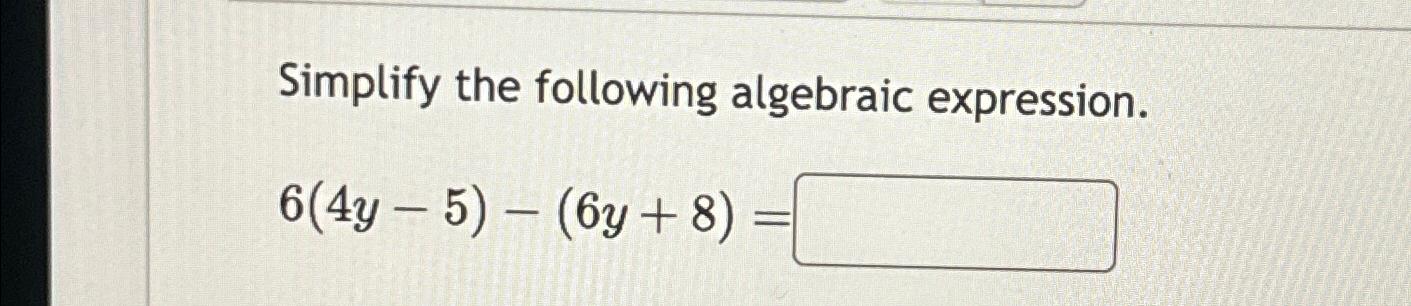
Algebra is often viewed as an abstract realm of numbers, letters, and symbols, yet it serves as the backbone of numerous mathematical concepts prevalent in our daily lives. Simplifying algebraic expressions is not merely an academic exercise; it reflects logical thinking and the ability to manipulate abstract ideas with precision. This article endeavors to elucidate the methodology underlying the simplification of algebraic expressions by engaging in a step-by-step analysis.
Before delving into the intricacies of simplification, it is paramount to grasp the foundational aspects of algebraic expressions. An algebraic expression, at its core, comprises variables, constants, and arithmetical operators. For example, in the expression 3x + 5, ‘3’ is a coefficient, ‘x’ is a variable, and ‘5’ is a constant. Understanding each component is crucial as it sets the stage for effective manipulation.
To embark on the simplification journey, one must first identify the type of expression at hand. Expressions can take various forms: linear, quadratic, or polynomial. Each requires distinct approaches for simplification. A linear expression, such as 2x + 3x – 4, can be simplified by combining like terms, while a quadratic expression may necessitate different strategies, such as factoring or applying the quadratic formula.
Let us delve into a linear example to appreciate the process of simplification. Consider the expression 2x + 3x – 4 + 5. The task here is to combine like terms systematically. The coefficients of ‘x’ can be summed:
- 2x + 3x = 5x
Next, we combine the constants:
- -4 + 5 = 1
Thus, the original expression simplifies to:
- 5x + 1
Once the expression has been simplified, one often seeks to ascertain its equivalence to another form. This leads us to the pivotal concept of equivalence in algebra. Two expressions are equivalent if they yield the same outcome for any value substituted for the variable. For instance, 5x + 1 is equivalent to 5(x + 0.2), reinforcing the notion that expressions exist in multifaceted forms yet retain intrinsic similarities.
To further explore equivalence, we can examine addition and multiplication in algebra. Consider the expression x(2 + 3) versus x*2 + x*3. This illustrates the distributive property, a vital algebraic principle that asserts the distributive nature of multiplication over addition. Recognizing such properties not only streamlines simplification efforts but also enriches one’s comprehension of algebraic structures.
As we strive for deeper understanding, we must also consider the importance of factoring as a simplification strategy. Factoring entails expressing a polynomial as a product of simpler polynomials. For example, the quadratic expression x² – 5x + 6 can be factored into (x – 2)(x – 3). This transformation is significant, as it facilitates easier evaluation and deeper insights into the expression’s properties.
Another dimension of algebraic expression simplification lies in the realm of rational expressions. These expressions contain variables in the denominator. Simplification of such expressions is often more complex, requiring a keen understanding of restrictions on variables. For instance, simplifying (2x²)/(4x) entails reducing the fraction by common factors. Here, we would cancel ‘2’ and ‘x’, yielding:
- (2x²)/(4x) = 1/2 as long as x ≠ 0
As we navigate through these algebraic transformations, it’s imperative to maintain vigilance towards domain restrictions. A savvy algebraist must ensure that any simplification performed does not inadvertently eliminate valid solutions. The analysis of rational expressions highlights the intricate balance between clarity and caution in mathematical manipulation.
Moreover, engaging with algebraic expressions opens doors to the exploration of inequalities. Simplifying inequalities, while conceptually akin to simplifying equations, often yields additional complexities. The critical understanding here is that multiplying or dividing each side by a negative value reverses the inequality sign. Hence, awareness of these subtle shifts is essential for accurate interpretation of simplified expressions.
Bridging these concepts to real-world applications reveals the prevalence of algebraic expressions in diverse fields, from engineering to economics. Simplifying expressions empowers professionals to model tangible scenarios effectively. Whether calculating costs, predicting outcomes, or optimizing performance, the ability to simplify and equate expressions is indispensable.
In conclusion, understanding how to simplify algebraic expressions is not simply an exercise in rote memorization or procedural application. It is a journey through the landscape of mathematical reasoning, where abstract ideas manifest in tangible forms. Each simplification opens up pathways for deeper analysis and broader applications, highlighting the elegance and utility of algebra. Mastery of these techniques instills confidence and fosters an appreciation for the power of logical thought, which transcends the confines of mathematics and permeates various aspects of life.
