Angles are fundamental geometrical elements that play a pivotal role in the study of shapes, lines, and the relationships formed therein. Understanding angles, particularly interior angles and the concept of adjacent angles, is vital not only in mathematics but also in various fields such as engineering, architecture, and even everyday problem-solving scenarios. In this article, we will elucidate the notion of adjacent interior angles and explore the categories of interior angles comprehensively.
Defining Interior Angles
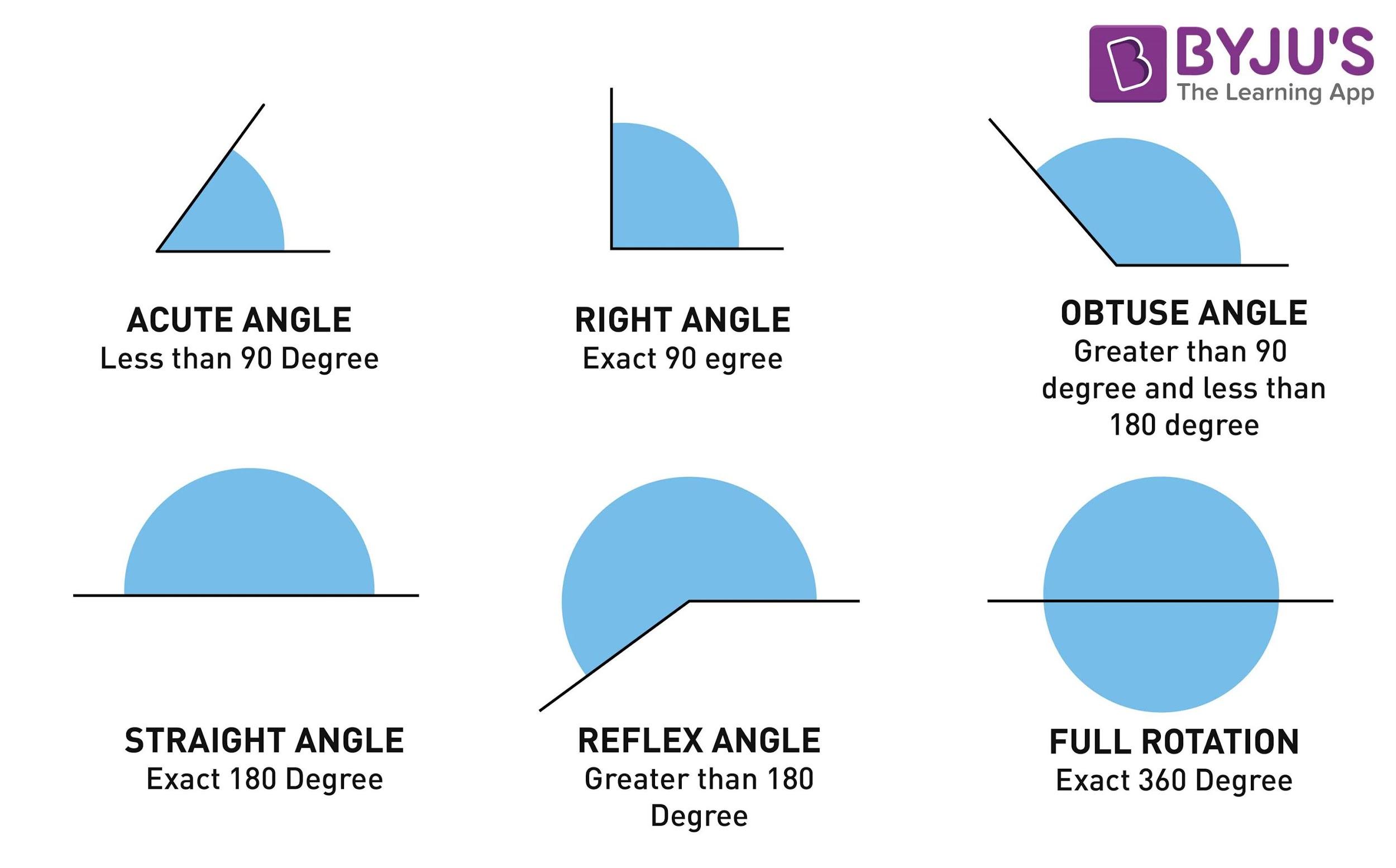
Interior angles are formed between two intersecting lines, meeting at a common point known as the vertex. These angles reside within a particular geometric shape, commonly polygons. The total measure of the interior angles depends on the number of sides of the polygon. For example, a triangle has three interior angles that sum up to 180 degrees, while a quadrilateral encompasses four interior angles summing to 360 degrees. Such relationships illustrate the remarkable order and predictability inherent in geometric principles.
Understanding Adjacent Angles
Adjacent angles are formed when two angles share a common vertex and a side. Critically, adjacent angles do not overlap, maintaining their distinction whilst being positioned next to each other. The position of these angles is significant within the broader context of geometry. One might visualize them as two angles that lean against a common ray, thereby establishing a cohesive spatial relationship.
Adjacent Interior Angles: A Deeper Insight
Adjacent interior angles inhabit the realm of interior angles and specifically refer to pairs of interior angles positioned adjacent to one another. To illustrate, consider a transversal line intersecting two parallel lines. The angles formed on the same side of the transversal within the two parallel lines are categorized as adjacent interior angles. Meanwhile, these angles maintain mutual exclusivity with respect to their adjacent counterparts, further enhancing the structural integrity of angles within geometric frameworks.
It is essential to recognize the intrinsic properties of adjacent interior angles. When the lines intersect, these angles often possess relationships governed by established postulates, such as the Alternate Interior Angles Theorem and the Consecutive Interior Angles Postulate. Such theorems suggest that adjacent interior angles may not only complement each other but can augment understanding regarding parallel lines and transversals, paving the way for complex geometric problem-solving tactics.
Examples of Adjacent Interior Angles
To better comprehend the concept, it is beneficial to examine real-world examples. Consider a scenario involving two parallel railroad tracks, intersected by a bridge-like structure (the transversal). Here we encounter adjacent interior angles that create acute and obtuse angles through their configuration. Not only do these angles illustrate the tenets of geometry, but they also serve as practical representations in design and engineering.
Similarly, within the context of a trapezium, where one pair of sides is parallel, adjacent interior angles formed with a transversal crossing the trapezium exemplify the relationships discussed. By analyzing such configurations, one can further grasp the implications of adjacent interior angles in both theoretical and practical applications.
Measurement of Interior Angles
Measuring interior angles is integral in both theoretical explorations and practical applications. Tools such as protractors offer a method to determine the degree measures of angles. However, understanding their interrelationships, particularly in the context of adjacent angles, provides a richer tapestry of knowledge. When investigating adjacent interior angles formed by a transversal intersecting parallel lines, it becomes apparent that these angles are supplementary, meaning their sum equals 180 degrees. Such principles amplify the study of angle properties and enhance analytical skills in geometry.
Applications of Adjacent Interior Angles
The implications of understanding adjacent interior angles extend beyond theoretical mathematics. In architecture, for instance, the principles governing adjacent interior angles influence structural design, ensuring stability and aesthetic appeal. In engineering, the efficient design of components and systems relies heavily on knowledge related to angles, including their measurement and interrelationship.
Moreover, educators leverage the concept of adjacent interior angles when teaching geometry, employing visual aids and interactive tools to foster comprehension among students. Such methodologies not only enhance engagement but supply a tangible connection between abstract mathematical principles and their real-world applications.
Conclusion
In conclusion, the exploration of interior angles, especially adjacent interior angles, unveils an intricate web of geometric principles that underpin a wide range of disciplines. Understanding these angles enriches one’s ability to analyze geometric configurations effectively. The relationship between adjacent interior angles and other types of angles invites deeper inquiry into the vast realm of geometry. As you navigate through the intricacies of angles, the value of mastering these concepts becomes ever more apparent, laying a robust foundation for future mathematical endeavors.
