Throughout the vast landscape of mathematical understanding, angles serve as the fundamental building blocks upon which geometric realities are constructed. They represent the interplay between lines and planes, much like dancers weaving through a choreographed performance. Among these angles lies the concept of supplementary angles—two angles whose sum transcends into the harmonious realm of 180 degrees. The question arises: which angle stands as a supplement to a given angle? This inquiry not only illuminates the nature of angles but also fosters a deeper appreciation for their interrelations within mathematics.
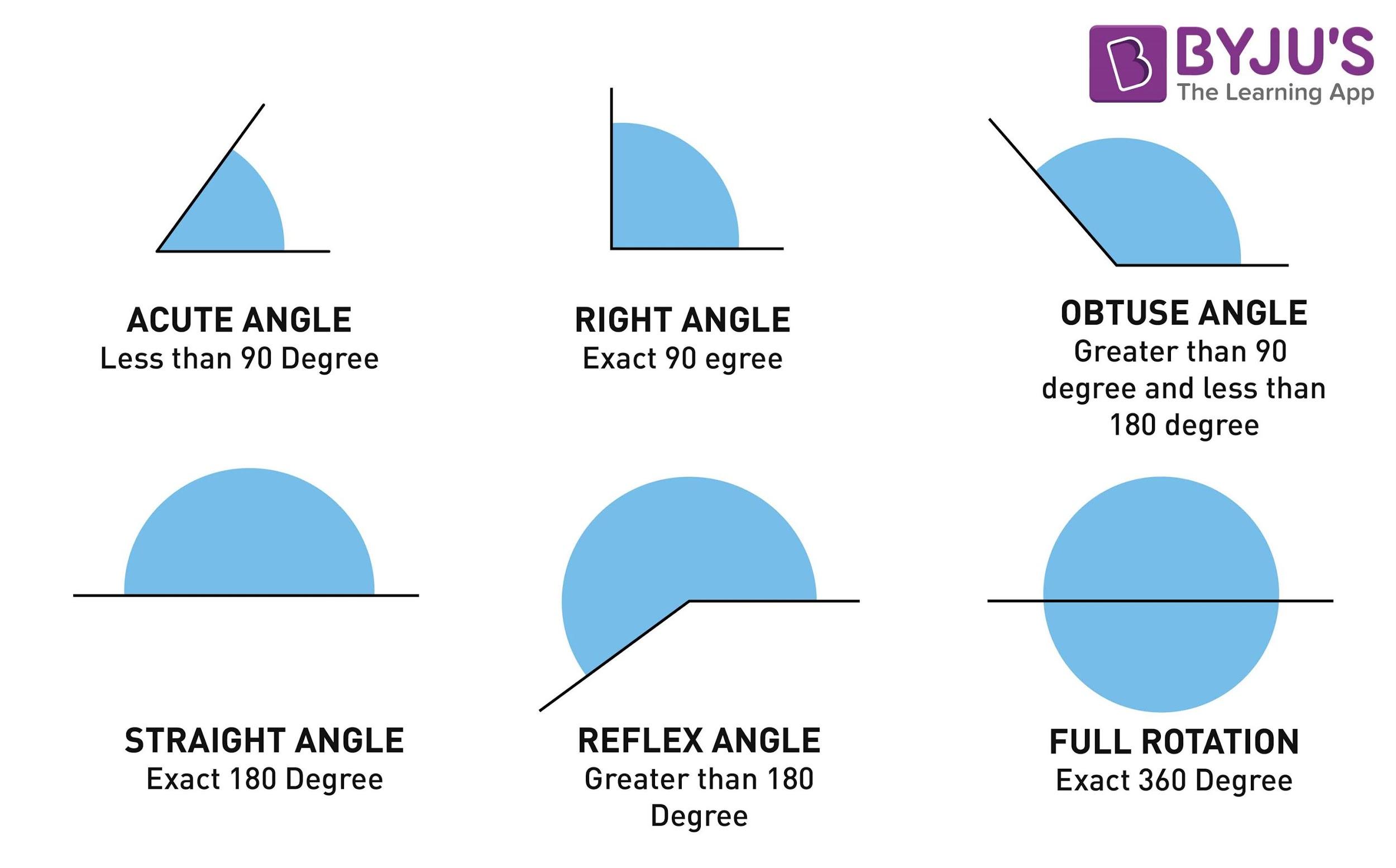
To unravel this concept, we must first establish a clear understanding of angle measurement. Angles are quantified in degrees, a unit that visualizes the rotation around a point. When two angles are described as supplementary, their measurements collectively yield the cardinal number of 180. This duo can vary from acute angles—less than 90 degrees—to obtuse angles—exceeding 90 degrees—but always they form a linear relationship that can be distinctly portrayed. Consider the analogy of a balanced scale: each angle acts as a weight, poised to counterbalance the other, ensuring equilibrium at a total of 180 degrees.
To illustrate this notion, let us consider a specific angle, denoted as ( x ). If one desires to identify its supplementary counterpart, one can approach the problem with the fundamental equation:
( x + y = 180^circ )
The variable ( y ) represents the angle that is supplementary to ( x ). To deduce ( y ), it’s a matter of simple algebraic manipulation:
( y = 180^circ – x )
This equation serves as a beacon, guiding one through the labyrinth of angle relationships. For example, if we take ( x ) as 70 degrees, the calculation reveals:
( y = 180^circ – 70^circ = 110^circ )
Thus, 110 degrees emerges as the angle that complements 70 degrees on this linear path, exemplifying the essence of supplementary angles.
However, to fully grasp the significance of supplementary angles, one must delve deeper into their manifestations in various geometric scenarios. In the context of polygons, particularly quadrilaterals, the relationship between angles becomes paramount. The interior angles of a quadrilateral, in their aggregate, amount to 360 degrees. Herein lie pairs of supplementary angles, forming one’s necessary foundation for understanding both simple and complex shapes. Every corner of a quadrilateral, each representing an angle, can potentially pair with its adjacent angle to maintain the equilibrium of geometry.
Consider the intriguing case of adjacent angles. When two angles share a common side and vertex, they often find themselves intertwined in a dance akin to complementarity. If one angle measures 45 degrees, its adjacent angle may well measure 135 degrees, together contributing to the grand total of 180 degrees. This not only emphasizes their interconnectedness but highlights how supplementary angles weave through the fabric of mathematical reasoning.
Furthermore, the beauty of supplementary angles extends beyond rigid geometric figures; it permeates the world of architecture, physics, and even art. In structural design, architects meticulously calculate angles to ensure the integrity and aesthetic appeal of their creations. The angles formed by beams and pillars must often be supplementary to uphold the principles of balance and symmetry. A well-crafted structure mirrors the precision of angles, showcasing the inherent elegance of mathematical concepts.
In physics, the concept of angles manifests within the discussions of forces and vectors. When analyzing forces acting on an object, one may encounter angles that, when summed with opposing angles, yield essential equilibrium states. Thus, mathematics acts as a crucial lingua franca, bridging the domains of science and art through the lens of angles.
While engaging with supplementary angles, one discovers not only mathematical facts but also profound metaphors and lessons. The partnership formed between two supplementary angles exemplifies collaboration and unity. With every angle serving as an individual entity, the need for cooperation becomes apparent. A single angle may achieve eloquence, but it is the union of pairs that transcends to create something greater—akin to two minds coming together in harmonious agreement, reaching a conclusion greater than the sum of their parts.
As one embarks on this mathematical exploration, it becomes essential to view angles not merely as isolated entities, but as integral components of a larger tapestry. Supplementary angles embody the principles of balance and coexistence, revealing the symbiotic relationship that characterizes the universe of geometry. When posing the question of which angle is supplementary, we embrace the invitation to explore mathematical possibilities, bridging complexity and simplicity in a dance of angles.
In conclusion, supplementary angles represent a unique interplay within the mathematical realm—where precision, beauty, and utility converge. The identification of complementary angles requires not just calculation but a conceptual understanding steeped in the principles of geometry. Whether navigating a classroom, designing a building, or applying theory in a scientific context, the significance of supplementary angles manifests as an essential thread woven into the fabric of mathematics, illustrating that even the simplest concepts can yield profound insights when approached with curiosity and wonder.
