The angular momentum quantum number, often denoted as ( l ), plays an indispensable role in delineating the sublevels within an atom’s electronic structure. The connection between angular momentum, quantum mechanics, and atomic theory is profound, and its implications extend far beyond mere academic interest. This article endeavors to elucidate the characteristics provided by the angular momentum quantum number, alongside its significance in the grand tapestry of atomic structure.
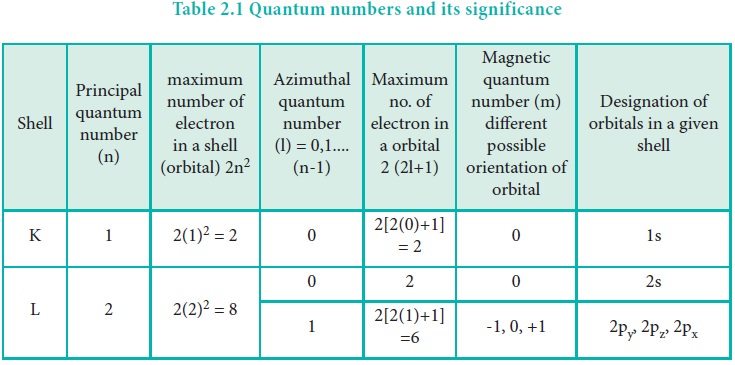
To appreciate the importance of the angular momentum quantum number, we must first establish its place within the quantum mechanical model of the atom. Electrons in an atom inhabit discrete energy levels, characterized by several quantum numbers — principal quantum number ( n ), angular momentum quantum number ( l ), magnetic quantum number ( m_l ), and spin quantum number ( m_s ). Among these, ( l ) specifically provides insight into the shape of the electron cloud and the orientation of orbitals, thereby influencing numerous physical and chemical properties of atoms.
The value of the angular momentum quantum number can take on integer values starting from ( 0 ) up to ( n-1 ). For instance, if an electron resides in the second energy level (( n=2 )), the possible values of ( l ) are ( 0 ) and ( 1 ). Each corresponding value of ( l ) denotes a different type of orbital: ( l = 0 ) represents an s orbital, ( l = 1 ) corresponds to a p orbital, and so forth. These orbitals possess unique shapes — spherical for s orbitals and dumbbell-shaped for p orbitals — highlighting the spatial distribution of electron density around the atomic nucleus.
This spatial characteristic impacts several phenomena observed in atomic behavior. The orientation and shape dictated by ( l ) directly influence how atoms interact with one another during chemical bonding. For instance, the presence or absence of certain orbitals can determine the ability of an atom to form specific types of bonds, such as ionic or covalent bonds. The underlying cause of these interactions often stems from electron-electron repulsions and the need for stable configurations, underscoring a deeper reason for fascination with the angular momentum quantum number.
Furthermore, the angular momentum quantum number sets the stage for quantized angular momentum, a concept that signifies the inherent restrictions on the values that angular momentum can adopt. In quantum mechanics, the angular momentum associated with an electron in an atom is quantized into discrete units, and the angular momentum quantum number quantifies this quantization. More specifically, the angular momentum of an electron can be represented by the formula ( L = sqrt{l(l + 1)} hbar ), where ( hbar ) is the reduced Planck’s constant. This intrinsic property of quantization is a fundamental concept in quantum mechanics and informs many aspects of atomic theory.
Moreover, ( l ) influences the energy levels of the orbitals themselves. Within a given principal energy level, the sublevels corresponding to different ( l ) values have varying energies; for instance, in hydrogen-like atoms, the ordering of energy levels is typically s < p < d < f. This hierarchical arrangement allows for the understanding of how electrons fill orbitals according to the Aufbau principle, ultimately leading to the formation of the periodic table and the distinctive chemical properties exhibited by the elements.
The angular momentum quantum number also opens up avenues for exploring the complex behavior of multi-electron systems. In many-electron atoms, electrons exhibit interactions that can lead to subtle shifts in energy levels, known as electron-electron repulsion effects. The interplay between ( l ) values within these systems can manifest as splitting of energy levels, phenomena that are pivotal in spectroscopy and in understanding the emission and absorption spectra of elements. These spectral lines provide tangible evidence of an atom’s electronic structure and are fundamental to fields such as astrophysics and chemical analysis.
In addition to its implications for bonding and energy levels, the angular momentum quantum number challenges our perception of atomic behavior. The intricate dance of electrons guided by quantum mechanical principles beckons researchers and enthusiasts alike to delve deeper into the subtleties of their interactions. The quantum number ( l ) not only classifies electrons into orbitals but also embodies a complex web of physical phenomena, highlighting the interconnectedness of various atomic properties.
Ultimately, the quest to understand the characteristics imparted by the angular momentum quantum number serves as a gateway to unraveling the mysteries of atomic structure. Its role in defining orbital shapes and energies, alongside its influence on electron interactions and chemical properties, captivates the imagination and deepens our appreciation for the atomic world. From the formulation of quantum mechanics to the development of new materials and technologies, the insights gleaned from exploring ( l ) are both profound and far-reaching. As we continue to probe the intricacies of atomic behavior, the angular momentum quantum number remains a cornerstone of our understanding, inviting continuous exploration and innovation.
