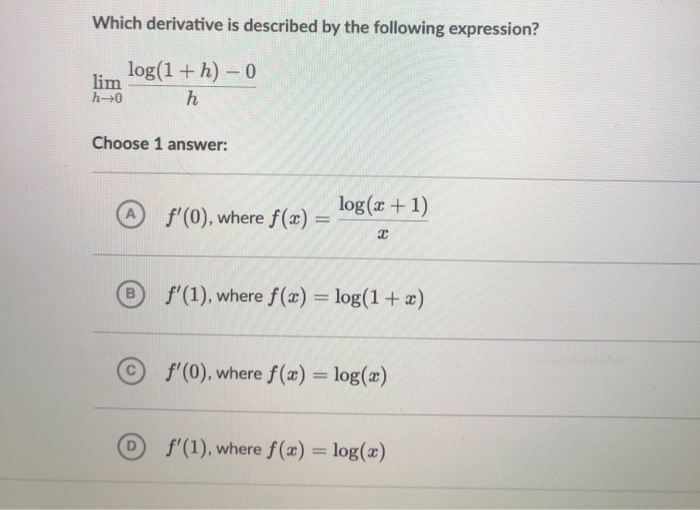
Understanding derivatives is fundamental to calculus, with applications spanning various fields, including physics, economics, and engineering. The query “Which derivative is described by the following expression?” prompts a deeper examination of calculus and its various branches. This exploration not only elucidates the meaning of derivatives but also categorizes the types of derivatives one may encounter. This article provides a comprehensive overview of derivatives, their classifications, and their significance in mathematical analysis.
1. Defining Derivatives
At its core, a derivative evaluates the rate at which a function value changes as its input changes. Formally, if ( f(x) ) is a function, the derivative ( f'(x) ) indicates how ( f(x) ) varies with ( x ). Consequently, the derivative can be seen as a function that provides instantaneous rates of change. This is mathematically defined via limits, expressed as:
$$f'(x) = lim_{h to 0} frac{f(x+h) – f(x)}{h}$$
This formula encapsulates the fundamental essence of a derivative as it approaches the secant line’s slope between two points on the graph, converging to the tangent line as the distance between the points diminishes.
2. Types of Derivatives
Derivatives can be classified into several categories, each serving specific purposes and contexts. Below, we delineate the most prominent types:
2.1. Ordinary Derivatives
Ordinary derivatives pertain to functions of a single variable. They offer insights into local behavior, including increasing and decreasing functions, points of inflection, and local maxima or minima. Important applications include physics for motion analysis, where the derivative of position with respect to time yields velocity.
2.2. Partial Derivatives
Partial derivatives are employed in functions with multiple variables. Denoted as ( frac{partial f}{partial x} ) for variable ( x ), they measure how ( f ) alters concerning one variable while holding others constant. This concept is vital in fields such as thermodynamics and fluid dynamics, where systems depend intricately on various interrelated variables.
2.3. Higher-Order Derivatives
Higher-order derivatives involve iterating the differentiation process. The second derivative, denoted ( f”(x) ), represents the rate of change of the first derivative. It conveys information about the curvature of the function’s graph. Higher-order derivatives are insightful in Taylor series expansions and physics, particularly in acceleration analysis.
2.4. Implicit Derivatives
In many real-world scenarios, functions cannot be expressed explicitly in ( y = f(x) ) form, necessitating implicit differentiation. By applying differentiation principles to both sides of an equation, one can derive relationships between variables that are not straightforward. This tactic is prevalent in complex mathematical modeling.
2.5. Directional Derivatives
Directional derivatives extend the concept of partial derivatives by considering the change in a multivariable function in a specific direction. It is calculated using the dot product of the gradient vector and the direction vector. This derivative is particularly advantageous in optimization problems where the steepest ascent or descent in a multidimensional space is sought.
3. Applications of Derivatives
Derivatives are not purely theoretical constructs; they have innumerable applications across various domains:
3.1. Optimization
Derivatives are instrumental in finding optimal values in minor and critical function analysis. By analyzing critical points determined by setting the first derivative to zero, one can identify local maxima and minima, essential in economic modeling and resource management.
3.2. Motion Analysis
In the physical sciences, the relationship between position, velocity, and acceleration is defined through derivatives. The derivative of the position function gives velocity, while the derivative of the velocity function gives acceleration, creating a profound connection between calculus and physics.
3.3. Engineering Design
Derivatives facilitate engineering calculations concerning rates of change. Whether analyzing structural loads or optimizing designs for efficiency, derivatives help engineers predict behaviors and improve system performance.
4. Further Considerations
Multiple approaches exist for calculating derivatives, including analytical techniques, the power rule, product rule, and quotient rule, which streamline the differentiation process. As one delves deeper into the discipline, numerical derivative approximations, like the finite difference method, also offer significant insights, particularly in computer simulations where analytical solutions are intractable.
5. Conclusion
Understanding derivatives and their diverse types is essential for anyone engaging in calculus. By recognizing the various classifications—from ordinary to directional derivatives—and their applications across multiple disciplines, one can appreciate the profundity of change delineated by these mathematical tools. The study of derivatives not only elucidates mathematical phenomena but also enriches our comprehension of the world, underscoring their importance across scientific and applied fields.
