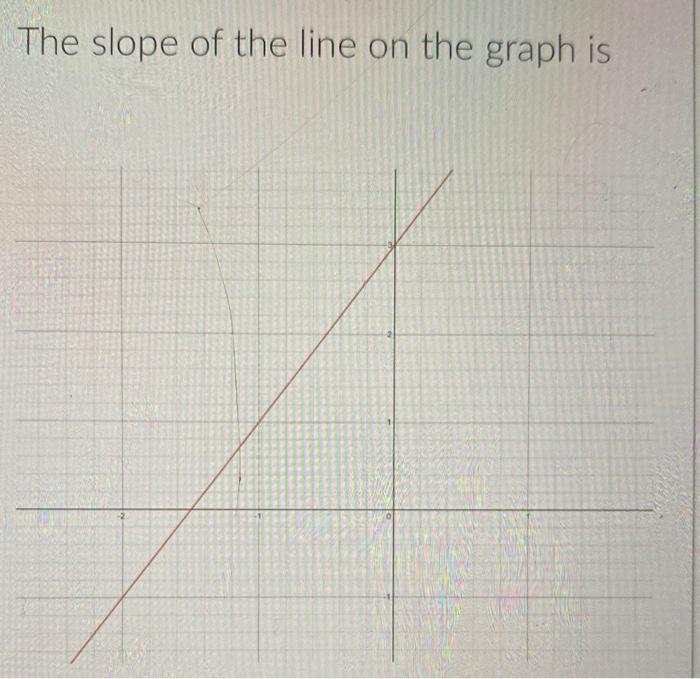
The concept of slope is paramount in the study of graphing linear equations and understanding relationships between variables. At first glance, a line on a graph may seem like just a simple visual representation of information; however, delving deeper into its slope can reveal profound insights into the nature of relationships depicted. Slope serves as a measure of the steepness, inclination, or gradient of a line. This article offers an extensive exploration of the slope of the line in a graph, exploring its definition, significance, calculation methods, and implications across various fields.
Defining Slope
The slope of a line can be quantitatively expressed as the ratio of the vertical change (rise) to the horizontal change (run) between any two points on the line. Mathematically, it can be denoted as follows:
Slope (m) = (change in y) / (change in x) = (y2 – y1) / (x2 – x1)
In this expression, (x1, y1) and (x2, y2) represent two distinct points on the line. The outcome of this calculation can vary: a positive slope signifies an upward trend, while a negative slope indicates a downward movement. A slope of zero implies a horizontal line, whereas an undefined slope corresponds to a vertical line.
The Significance of Slope
Slope is not merely a mathematical abstraction; it holds significant implications in various real-world contexts. In economics, for instance, the slope of a demand curve indicates the relationship between the price of a commodity and the quantity demanded, providing crucial insights for businesses and policymakers. In physics, slope can represent speed when time is plotted on one axis and distance on another. Understanding slope in these contexts promises a deeper comprehension of the dynamics at play.
Interpreting Positive and Negative Slopes
To elucidate further, let us consider the distinctions between positive and negative slopes. A positive slope reveals that as one variable increases, the other variable also ascends. This correlation often reflects beneficial relationships, such as income and expenditure, where higher income can lead to increased spending. In contrast, a negative slope suggests an inverse relationship. As one variable rises, the other declines. For example, an increase in prices might lead to a reduction in quantity demanded, which mirrors the law of demand in economic theory.
Understanding Zero and Undefined Slopes
A slope of zero presents an intriguing scenario, representing a line that remains perfectly horizontal. This condition occurs when the dependent variable does not change despite variations in the independent variable; one might interpret this as a state of equilibrium. Conversely, an undefined slope is represented by a vertical line—here, the independent variable remains constant while the dependent variable changes freely. This concept can be challenging yet captivating, as it implies a unique relationship where one variable stands resolute while the other is unrestrained.
Calculating Slope from Data Points
Calculating the slope between two points on a graph is straightforward, yet understanding how it fits within larger datasets invites a broader exploration. To calculate slope effectively, one must delineate points and scrutinize the corresponding coordinates. This capability can be particularly advantageous in empirical research, where data trends are evaluated. In practice, researchers can apply regression analysis, a sophisticated tool that allows for the calculation of the slope within scatter plots and various statistical models, thereby discovering relationships obscured within the noise of random data.
Slope in Different Mathematical Contexts
Beyond linear relationships, the concept of slope manifests in nonlinear contexts as well. For instance, in calculus, the concept of the derivative defines the slope of a curve at any given point. This infinitesimal analysis lends itself to interpretation in physics and engineering, where instantaneous rates of change are critical for modeling complex systems. The multifaceted nature of slope enriches an individual’s understanding of dynamic systems, allowing for predictions and optimized solutions.
Visualizing Slope
The graphical representation of slope can often enhance comprehensibility. By visualizing lines on a Cartesian plane, one can immediately interpret inclinations. The steeper the line, the greater the slope; conversely, a gently sloping line indicates a minimal slope. Using graphing software can further elucidate trends, facilitating a practical understanding of linear equations and their slopes.
The Broader Implications of Understanding Slope
The implications of understanding slope extend far beyond the classroom. In fields such as environmental science, climate change models often incorporate slope to illustrate changes in temperature or precipitation rates. Similarly, slope plays a vital role in healthcare by elucidating relationships between variables such as age and blood pressure. By grasping the slope, professionals can make informed decisions that positively impact lives.
Conclusion
In summary, slope is a cornerstone of mathematical and empirical analysis, weaving its significance into the very fabric of countless disciplines. The ability to analyze slope fosters intuition about relationships, enabling predictions and informed decision-making. As one becomes adept in interpreting slopes, the promise of a deeper understanding of the interconnectedness of data and trends emerges. Embracing this knowledge can certainly shift one’s perspective and nurture curiosity, revealing the hidden narratives encapsulated within the lines of a graph.
