The trajectory of a projectile, such as a rock thrown into the air, embodies a remarkable interplay of physics, mathematics, and natural phenomena. Understanding this trajectory is not only crucial for those studying the principles of physics but also for anyone fascinated by the mechanics of motion in the natural world. This article delves into the intricacies of projectile motion, exploring the factors that influence a rock’s trajectory and the various diagrammatic representations that can visualize this motion.
When one casts an object skyward, several forces come into play. First and foremost is gravity, continually acting upon the object and pulling it downward. Another pivotal element is the initial velocity at which the object is projected. This velocity can be broken down into two components: the horizontal and the vertical. Collectively, these components determine the parabolic path typically associated with projectiles. Understanding these basic principles lays the groundwork for analyzing which diagram accurately represents a rock’s trajectory.
Projectile motion can be encapsulated by two fundamental equations: those governing horizontal and vertical motion. The horizontal distance covered by the projectile, or range, can be expressed as a function of its initial velocity, with no acceleration acting upon it in the horizontal direction (ignoring air resistance). In contrast, vertical motion is influenced by acceleration due to gravity, typically approximated as 9.81 m/s² downwards. The combination of these two motions results in a characteristic trajectory that is parabolic in shape.
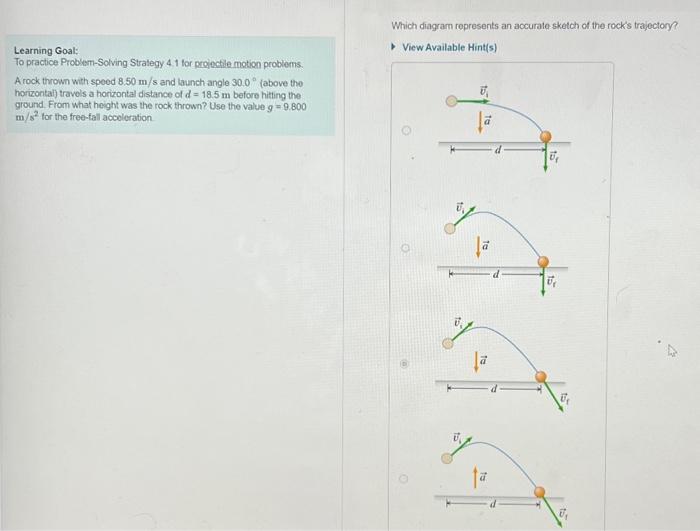
To accurately represent a rock’s trajectory, a diagram must incorporate both the horizontal and vertical components of motion. A quintessential illustration would delineate the initial launch angle, often related to the horizontal surface from which it is projected. This angle is particularly significant; it dictates not only the height achieved by the rock but also the distance it will travel before descending back to the ground. Common launch angles include 30°, 45°, and 60°, each yielding various outcomes in terms of range and altitude.
Furthermore, drag forces emanating from air resistance must not be disregarded. While introductory analyses often assume a vacuum where only gravitational forces act, real-world applications necessitate an understanding of how air resistance influences the trajectory. High-velocity objects, such as stones thrown with force, encounter drag that results in a trajectory differing from the ideal parabolic path. Consequently, a diagram representing a rock’s trajectory in practice will often portray a less symmetrical arc, where the descent curve steepens due to decreased velocity as air resistance overcomes the forces exerted by the initial throw.
The relationship between the launch angle and the resultant trajectory reveals a deeper fascination with the dynamics of movement. For instance, the optimal launch angle for achieving maximum range in a vacuum is typically 45°. However, due to the complexities introduced by air resistance, this angle shifts slightly for practical applications. Thus, when scrutinizing diagrams, one must pay close attention to the associated angle and how it interacts with forces at play during the launch and descent phases.
Moreover, various types of diagrams illustrate the rock’s trajectory in differing contexts. A basic scatter plot might illustrate individual launches across varied angles and their corresponding ranges, whereas a more complex simulation could incorporate animated vectors demonstrating the shift in trajectory as air resistance alters the motion over time. Each representation offers insights into the nature of projectile motion, emphasizing the multifaceted nature of seemingly simple actions.
In examining diagrams, one must also consider the referencing of key points along the trajectory—namely, the apex, or peak height, of the rock’s flight. The apex serves as a crucial marker, indicating the transition from upward motion to downward motion, and signifies the highest point achieved during the flight. Accurate diagrams will highlight this peak and provide a visual correlation between the initial velocity, angle of launch, and the apex height reached.
Furthermore, an astute observer might note how external factors such as wind velocity and altitude can influence the rock’s trajectory, prompting further inquiries into how variations in these elements may provide additional complexities to the diagram. This intricate relationship between measurable factors adds layers to the categorical understanding of projectile motion, inviting an exploration into ever-evolving environments.
In summary, accurately representing a rock’s trajectory through diagrams requires a comprehensive understanding of the forces involved in projectile motion. A proficiently constructed diagram encompasses the initial conditions—including launch angle and velocity—as well as the effects of gravity and air resistance, culminating in a visual representation that is both informative and accessible. As one contemplates the various illustrations of this phenomenon, it becomes evident that the simplicity of a rock’s flight belies a complex tapestry of physics at work, sparking a deeper appreciation for the forces of nature that govern our world.
Through the careful examination of trajectory diagrams, one is reminded of the elegance embedded within the laws of motion. The fascinating interplay of forces, angles, and velocities not only serves educational purposes but also invites a broader curiosity about how similar principles manifest across diverse scenarios in our environment. Ultimately, the pursuit of understanding rock trajectories encapsulates much more than the mechanics of motion; it appeals to an innate desire to comprehend the world around us.
