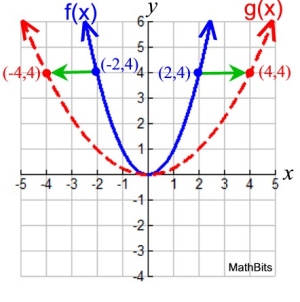
In the vast landscape of mathematics, functions serve as the bedrock upon which countless applications are constructed. Among these functions, transformations offer a mesmerizing perspective on how the world around us can be manipulated through simple mathematical principles. When we delve into the concept of horizontal stretches, we unveil a unique element of these transformations that can resonate with students and enthusiasts alike. The allure of a horizontal stretch lies in its ability to stretch a function, much like an artist elongating their canvas to capture an expansive panorama. This article will explore the phenomenon of horizontal stretching, elucidating its intricacies and characterizing the functions that embody this transformation.
At its core, a horizontal stretch refers to the expansion of a function along the x-axis. To grasp this notion, one must first understand the basic format of a function, commonly expressed as f(x). The transformation emerges when we introduce a multiplicative factor that modifies the input variable. Specifically, the function can be represented as f(kx), where k represents the stretch factor. When the value of k falls within the range of 0 < k < 1, the function experiences a horizontal stretching, and when k > 1, the function is, conversely, compressed.
Consider a quintessential example: the quadratic function f(x) = x². The graph of this function is a parabola that opens upwards in a characteristic manner. When we apply a horizontal stretch by altering the input, say to f(0.5x), the result is a parabolic curve that sprawls outward. Picture a rubber band being pulled in two directions; the individual points along the curve are coaxed away from one another, creating a wider and more expansive form. This is the visual manifestation of a horizontal stretch.
The unique appeal of horizontal stretching lies not only in its representation on a graph but also in the manner it influences the behavior of the function. For instance, consider the effect of stretching on the function’s roots or intercepts. In our earlier example of f(0.5x), the roots of the function, or the x-values where the graph intersects the x-axis, also experience transformation. The original roots are altered, yielding new positions that reflect the expanded nature of the graph. Thus, the mathematical journey illustrates transformation; stretching the function unfolds a new narrative of its roots, posing questions about the underlying relationships within the function itself.
To deepen this exploration, we can examine various types of functions, each displaying its distinctive behavior when subjected to horizontal stretches. Polynomial functions, such as cubic or quartic equations, similarly respond to transformations. For example, a cubic function f(x) = x³, when stretched to f(0.5x), transforms from an s-shaped curve into a more subdued and flattened form. The dominance of x-values hence appears more pronounced, revealing the intricate balance between the coefficients and the inputs, akin to a symphony where the harmony unfolds dramatically with newfound tempo.
Understanding the nuances of trigonometric functions reveals yet another dimension of horizontal stretching. The sine function, f(x) = sin(x), is a wave-like graph, oscillating between -1 and 1. When manipulated into f(0.5x), the frequency of the wave diminishes—the peaks become more leniently spaced. This adjustment imparts a lyrical quality to the wave, evoking a sense of tranquility akin to the slow undulations of a serene ocean rather than the frenetic motion of a rapid stream. Here, horizontal stretches unveil the underlying rhythm of the cyclical nature of trigonometric functions.
The ramifications of horizontal stretching extend beyond aesthetic changes; they resonate throughout calculus, touching upon the fundamental principles of limits, derivatives, and integrals. The effect of stretching on the curve places particular emphasis on the rate of change, as it effectively influences the derivative of the function. This connection reinforces the importance of understanding transformations within the broader mathematical framework. The implications of horizontal stretches illuminate the interconnectivity among various branches of mathematics, akin to the threads that weave a rich tapestry.
As one continues to unravel the intricacies of horizontal stretches, it becomes increasingly clear that these transformations play a crucial role in modeling real-world phenomena. In fields such as physics and economics, where mathematical functions are employed to represent relationships and behavior, a thorough comprehension of horizontal stretching equips individuals with the tools needed to analyze and interpret complex systems. The ability to stretch a function offers the power to glean insights and predict outcomes across diverse disciplines.
In conclusion, horizontal stretches are not merely mechanical adjustments but rather provocative alterations that breathe new life into functions. The exploration of these transformations allows one to appreciate the fluidity and dynamism inherent in mathematics. Much like an artist reinterpreting their subject matter, when functions are stretched horizontally, they reveal uncharted territories—new relationships, behaviors, and insights. As we embrace the artful dance of functions and their transformations, we cultivate a deeper appreciation for the elegance that lies within the mathematical universe, encouraging curiosity and exploration. Mathematics, then, becomes not just a study of numbers and equations, but a vivid journey through uncharted landscapes of thought and understanding.
